开普勒个人资料简介 开普勒的行星运动定律(2)

开普勒个人资料简介

获得以上重要但错误的结论之后，开普勒重新回到了火星的运动学。他首先提出了确定任意时刻火星的位置问题。

这需要给出火星运动经过的路程如圆弧QM和火星从Q到M所需的时间之间的关系（见图6.1）。这对当时的数学而言是不可能的。

于是开普勒采取了如下近似法。圆弧上一点M处的速度与MS成反比。

因此，通过M处一定长度的弧所需要的时间可用MS的长度来表示。这样一来，通过弧QM所需要的时间是动径MS的和。

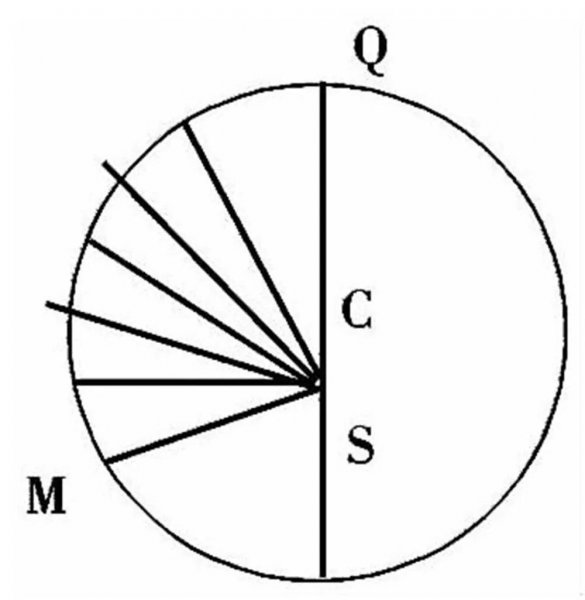
按照阿基米德的理论，动径之和就是扇形的面积。但是阿基米德的这个结论只有在S位于圆心C处时才正确。

而开普勒却大胆认为它在偏心圆的情况下也成立，于是给出了动径扫过的面积与时间的关系：成正比。

从推理过程来看这是一个很粗糙的结论，但开普勒由此得到了面积速度恒定的定律（开普勒第二定律）。

开普勒就这样找到了计算给定时刻的行星位置的方法。

据此，从给定的三个位置就能计算出该行星的远日点位置、偏心率。开普勒挑选了火星的几组三个位置进行计算，发现结果互相不一致。

于是开普勒抛弃了从柏拉图以来把天体看做沿圆形轨道运动的信条，并得出结论说：火星轨道不可能是圆形。

为了找到正确的轨道形状，开普勒起先考虑卵形轨道，但计算结果难以与面积定律符合。

后来他尝试椭圆，经过冗长的计算和“简直发疯似的思索”，最后确认，唯有椭圆才是火星的轨道。

并且，开普勒再次大胆地把从火星得来的规律推广到所有行星。

一个世纪以前，哥白尼已经开始寻找满足几何简单性要求的行星系统。

开普勒解决了哥白尼的问题，他所达到的简单性在天文学史上超出了前人的梦想——仅仅一种圆锥曲线就足以描述所有行星的轨道。偏心圆和本轮的全部复杂性淹没在椭圆的简单性中了。

当然接受椭圆简单性是有代价的，那就是抛弃圆及其拥有的完美无缺、不易性和有序性的古老内涵。

开普勒心中也许从来没有忘记圆所具有的诱惑力。在他看来，面积定律的价值在于它提出了新的一致性来取代圆周运动的一致性。

我们既可以说开普勒完善了哥白尼学说，也可以说他破坏了哥白尼学说。

在1609年出版的《新天文学》中，开普勒发表了行星运动的第一定律和第二定律；在1619年出版的《宇宙和谐论》中他进一步发表了行星运动的第三定律。

这三条行星运动定律现在一般表述为：

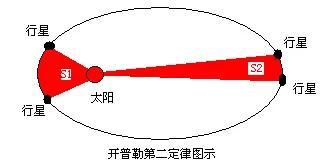
1.行星沿椭圆轨道绕太阳运动，太阳位于椭圆的一个焦点上。

2.从太阳到行星的矢径在相等时间里扫过相等的面积。

3.各行星公转周期的平方与轨道半长径的立方成正比。

它们被称做开普勒定律，为牛顿发现万有引力定律奠定了基础。

上面(「领啦网」)为您介绍的开普勒的行星运动定律及其开普勒个人资料简介的详细讲解，希望本文能给你带来生活上的帮助！