线性与非线性的区别解析 线性和非线性两者的差异和特点

线性与非线性的区别解析

一篇很详细的介绍是关于线性和非线性两者的差异和特点和线性与非线性的区别解析的相关知识，如有不对的地方欢迎指正！

线性与非线性的区别解析

线性和非线性是数学中常用的概念，其本质区别在于它们所遵循的规律不同。在实际应用中，我们常常需要对不同种类的数据或现象进行分类和分析，而线性和非线性则是这个分类和分析的基础。本文将从定义、特点以及实际应用等方面对线性和非线性进行解析。

定义

线性和非线性是两种表示变量之间关系的方式。在数学中，当变量之间的关系可以用一条直线来表示时，这种关系被称之为线性关系；而关系不能用一条直线表示的，就被称之为非线性关系。

线性

线性关系的数学表达式通常采用以下形式：y = a x + b。其中a和b都是常量，而x和y则是变量。如下图所示，当x和y之间的关系可以用一条直线表示时，它们的关系就是线性的。

非线性

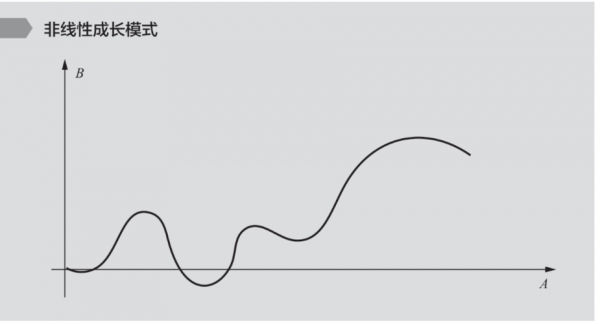
与线性关系相对应的是非线性关系。非线性关系包括多种种类，如二次函数、三次函数、正弦函数等等。下图是一个非线性关系的例子：

在这个图中，无法用一条直线来表达x和y之间的关系，因此该关系就是非线性的。

特点

线性和非线性各有其独特的特点，下面我们来逐一了解。

线性

线性关系中，自变量的变化对应着因变量的相应变化，而且这种变化是固定的比例关系。比如说，如果y = 2x + 3，那么x每增加1，y就会增加2。

这种变化规律是恒定的，即使x变化的极小，y也会随之偏移一定的量。线性关系还具有可加性和可分离性，即如果一个线性关系可以分解成两个或多个线性关系，那么这些关系之间是相互独立的，可以分别进行研究。

非线性

在非线性关系中，自变量的变化并不一定对应着因变量的相应变化。这种变化规律通常是复杂和不确定的，而且不能用一个简单的比例关系来概括。非线性关系不具备可加性和可分离性，因此我们需要特别注意非线性关系中不同因素之间的相互作用。

实际应用

线性和非线性在实际应用中有着广泛的用途，下面我们来了解一些应用案例。

线性

线性关系在物理学、经济学、工程学等领域中有着广泛的应用。比如说，在运动学中，我们可以用一条直线来表示物体的运动轨迹；在经济学中，我们可以用线性方程来描述供需关系、价格关系等等；

在工程学中，我们可以用线性模型来预测材料的疲劳寿命、结构的承重能力等等。线性关系的应用领域非常广泛，几乎在各个科学领域中都可以看到它的身影。

非线性

与线性关系不同，非线性关系的应用更加特殊和具体。比如说，在化学领域，我们常常需要研究反应速率与反应物浓度之间的关系，而这种关系通常是非线性的；在医学领域，我们需要研究药物剂量与疗效的关系，这同样也是一个非线性关系。

非线性关系的应用领域比较具体，但是往往会涉及到某些关键问题，对于解决这些问题具有重要的意义。

总结

线性和非线性是数学中的基本概念，其本质区别在于它们所遵循的规律不同。线性关系具有固定的比例关系、可加性和可分离性等特点，在物理学、经济学、工程学等领域中有着广泛的应用；

而非线性关系则具有复杂和不确定的特点，不具备可加性和可分离性，在化学、医学等领域中更具有特殊性和具体性。了解线性和非线性的区别可以帮助我们更好地理解和分析各种现象和问题，在实际应用中更加游刃有余。

上述的关于线性和非线性两者的差异和特点以及线性与非线性的区别解析的详细内容了，希望能给您带来帮助！