三角形中心是什么的交点及性质 三角形交点及其性质

三角形中心是什么的交点及性质

一篇小知识，与您分享三角形中心是什么的交点及性质方面的内容，相关内容具体如下：

在数学中，三角形是一项重要的研究领域。在这一领域中，研究的重要对象之一就是三角形中心。三角形的中心是三条中垂线、三条角平分线、三条中线和三角形外心、内心、重心的交点，它们构成三角形的七个中心。

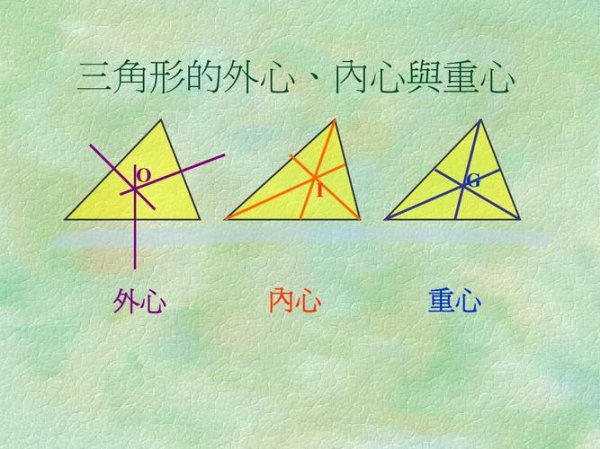
中垂线交点：垂心

中垂线交点也被称为垂心。在一个三角形中，垂心是三角形中心重要的一个点，也是直角三角形的一个重要特征。

垂心连接三角形的三个顶点分别与对边相交，形成三个垂线。这些垂线相交的地方就是垂心。

垂心可以用来计算三角形的各种属性，例如：三角形的高、垂直边、高点、外接圆、欧拉线等等。此外，在工程中，垂心还被用来测量高度和深度，是一项非常重要的计算方法。

角平分线交点：内心

角平分线交点被称为内心。在一个三角形中，内心是一个非常重要的点，它是到三角形三边距离之和最小的点。

也就是说，任何从其他点开始的线段，与三角形三边的距离和都大于从内心出发的线段。因此，在三角形题目中，内心往往是计算问题的关键。

内心还具有一些其他的性质。例如：内心到三角形三条边的距离相等；内心到三角形两条角平分线的距离也相等。此外，通过内心还可以推导出如内切圆半径、欧拉线等三角形相关的问题。

中线交点：重心

中线交点也被称为重心。在一个三角形中，重心是三条中线的交点，也是三角形内心到三边距离之和最小的点。

重心是三角形“重心”的来源，因为三角形相似于一个平衡的物体，它的重心能够保证三角形保持稳定。

重心还有一些其他的性质。例如：重心到顶点的距离等于三角形中线长度的一半。此外，重心还可以用来计算三角形的内切圆、外接圆、欧拉线等三角形相关属性。

外心

外心是指一个三角形的外接圆心。在一个三角形中，外接圆心是三角形外接圆的中心，也是三角形三条中垂线的交点。外接圆过三角形的三个顶点，其半径等于三角形的半周长除以其面积。

外接圆的半径可以用来计算三角形的面积、周长以及三边角度。此外，通过外心还可以推导出诸如三角形的勾股定理、圆的欧拉线等相关问题。

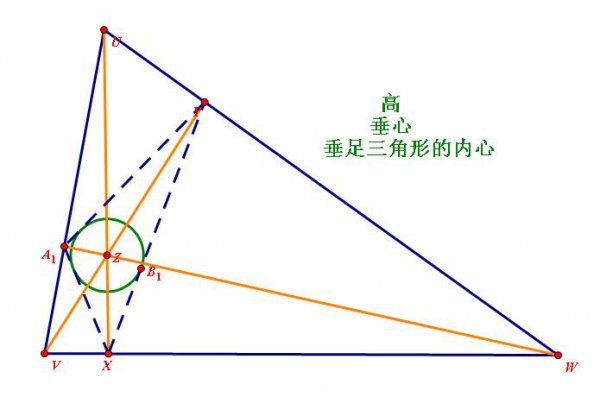
内心、外心、垂心、重心的关系

内心、外心、垂心、重心在三角形理论中都扮演着重要角色。它们不仅可以被用来计算三角形的各种性质，还可以帮助解决许多数学问题。

在三角形中，内心、外心、垂心、重心有一个非常重要的关系。它们都位于欧拉线上，也就是三角形三角心之间的一条直线。

欧拉线还有其他的一些性质，例如：内心到垂心的距离等于外心到重心的距离，欧拉线通过三角形的垂心、重心，以及外心、内心之间的中点。

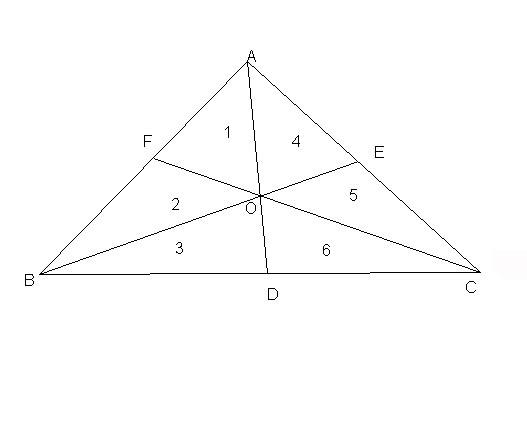
总结：

三角形中心是三角形理论中一个非常重要的概念。三角形的七个中心，即：内心、外心、垂心、重心、媒心、费马点、等角点，是求解三角形相关问题的重要工具。

本文介绍了四个最常见的中心点：垂心、内心、重心、外心以及它们之间的关系。希望对你在学习三角形相关问题时有所帮助。

以上就是三角形中心是什么的交点及性质的相关内容，希望对您有所帮助！