科研论文中p值和显著性水平的关系 P值及其计算方法(2)

科研论文中p值和显著性水平的关系

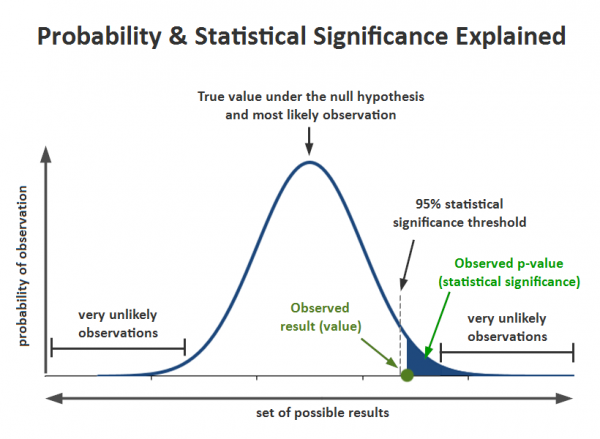
上图：概率及统计显著性示意。纵轴是观察的概率，横轴是结果可能的取值。

Very unlikely observations = 非常不可能的观察结果

Observed Result(value) = 观察结果（值）

95% statistical significance threshold = 95%统计显著性门槛值

Observed p-value (statistic significance) = 观察到的p值（统计学显著性）

用一个栗子小结一下

例如，我刚在"饿了吗"上点了一份餐，饿了吗估算的送达时间是30分钟，但我坚持认为通常30分钟内都送不到。

所以我可以进行一次 假设检验， 因为我认为"送达时间在30分钟以内"的 零假设 是不正确的，因此我的 对立假设 是"送达时间大于30分钟"（也就是说会迟到，要知道送餐迟到饿了吗就要赔优惠券，哈哈）。

为了证实我的观点，我每天都点这同一家餐馆，并实测每次送达所花的时间。

在获得了大量的样本数据之后，我计算了样本的P值，假设P值是0.001（远小于0.05），这意味着，我 关于"送餐会迟到的判断会是错误的"的可能性大概是0.001，或者说我判断错误的可能性远小于 0.05这个"统计学显著性的经验门槛值" 。

因此，我基本上可以相信饿了吗自动估算的时间是错的，这样一来饿了吗每次都应该给我赔偿优惠券。

但现实中这只是我的痴心妄想，基本上没可能，因为饿了吗公司的开发人员可没有那么傻。他们一定会根据每次送餐的送达时间的统计情况，不断刷新它们的估算公式，以确保他们估算结果的P值<>

饿了吗APP搜集的大数据会确保在绝大多数时间，送餐人员的的递送时间都不会超时（当然他们的算法可能会更复杂，统计学结论可能只是其中的一部分）。

如何对待统计学显著性对某项研究的意义？

置信度会因为一个重要的原因而降低—— 抽样误差， 它是数据扭曲的常见原因。显然，如果你研究基于的是有缺陷的数据，结论肯定不会正确。

例如，你希望调查大众最喜欢的食物。但是您跑到麦当劳去调查，那么结果可能是最喜欢吃牛肉汉堡；但如你跑到素餐厅去调查，结果就大不相同了。这就是一个被夸大了的 抽样误差 问题。但所有的抽样都会存在抽样误差，只是误差大小区别而已。

因此，统计上的显著性并不一定能保证客观上是正确的。 这就是我们经常发现一些貌似数据很有说服力的论文的结论被其他同类研究推翻的原因之一。

在科研领域， 统计显著性往往并不能完全断言研究人员的假设就是100%正确的，但往往能够告诉研究人员他的假设是有一定可信的事实基础的，值得进一步研究。

如何计算P值？

这个部分是写给有兴趣了解在统计学上P值是如何计算的读者的。如果您只是想粗浅地了解下P值和统计学显著性的概念，那么后面的内容就可以略看或者不看了。

计算并确定统计显著性有点复杂，往往实用中会用一些软件工具来计算，例如IBM的SPSS或者开源的Jamovi，这两者都是统计学分析工具。此外，网上还有一些在线计算器，主要有Z测试计算器和T测试计算器之类，专用于做显著性相关统计学评分的计算。

我在这里会介绍如何 手工 计算统计显著性 ，这里是采用t分数来获取P值：

步骤1：设定零假设和对立假设

先指出哪个是零假设（H0）。在科研中，零假设通常会被设定为实验措施无效，这意味着实验失败，也就是研究人员希望通过实验否定的那个假设。

零假设确定之后， 对立假设（Ha） 也就确定了——对立假设与零假设在逻辑上互否。在科研中，对立假设通常是说科研需要证实的那个措施，这意味着实验成功或者具有进一步研究意义。

例如，假设我们研究某种药物对病人的有效性。我们的零假设将是："这种药物对病患完全没有影响。" （既没有正向的影响，也没有负向的影响）

但通常测试药物是否有效是通过"实验组"样本与"对照组"样本的差别来确定的。对照组通常会给予"安慰剂"，这相当于没有服药（但是对照组的病人并不知道自己是否服用了有效的药物）。

如果实验组的结果与对照组没有差异，则表示药物无效。所以零假设可以转设为 "实验组和对照组没有差异"。因此，只要我们通过统计分析否定这个零假设，即可得出支持药物有效性的结论。

步骤2：选取α值

我们需要设定一个显著性门槛的级别，即前述α值，确切的说其含义是：某假设被认为可信时零假设可能成立的概率（这可能有点绕）。

通常α值选取为0.05（即5％）作为显著性的门槛，但不同实验敏感度要求不同。在某些领域的研究当中，可以提高显著性的门槛，诸如药物测试或精密仪器制造等等，对于这些领域，可能选取0.01更为合适。

由于置信度= 1-α（％），因此如果α值为0.05，那么达到此门槛的测试统计结果置信度就为95％。