全等三角形的定义 性质 判定

全等三角形的定义，性质，判定

今天介绍全等三角形的定义，性质，判定的介绍，一起来了解了解吧。

全等三角形的定义

全等三角形是指三边长度相等的三角形。根据勾股定理，如果一个三角形的三边长分别为a、b、c，那么满足条件：a² + b² = c²。

这样的三角形被称为直角三角形，其中最长的一条边称为斜边，其他两条边称为直角边。

全等三角形的性质

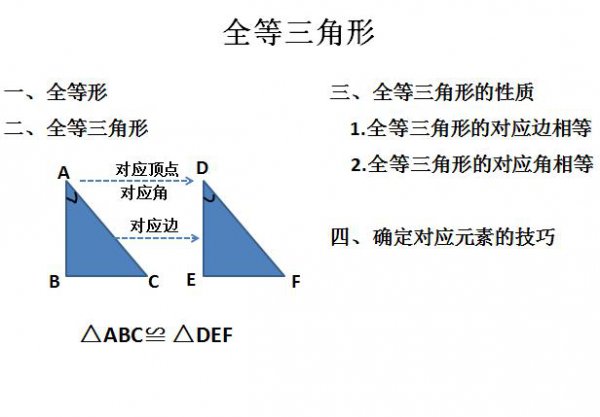
1. 全等三角形的三边长度相等。

2. 全等三角形的三边互相垂直。

3. 全等三角形的面积等于底乘以高除以2。

4. 全等三角形是对称图形。

5. 全等三角形的内角和为180度。

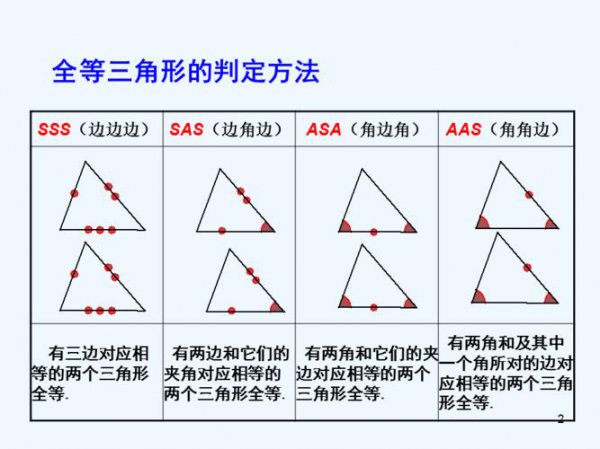
全等三角形的判定方法

1. 观察法：通过观察三角形的三边长度是否相等来判断是否为全等三角形。

2. 计算法：利用勾股定理计算三角形的三边长度，然后判断是否相等。

3. 比较法：将两个三角形的三边长度进行比较，看它们是否相等。

4. 证明法：通过数学证明或逻辑推理来判定三角形是否为全等三角形。

全等三角形的应用

1. 建筑领域：在建筑设计中，全等三角形常用于计算建筑物的面积和周长。

2. 几何学：在几何学中，全等三角形是研究空间几何的基本概念之一。

3. 工程学：在工程学中，全等三角形用于计算建筑物的结构强度和稳定性。

4. 计算机科学：在计算机科学中，全等三角形可以用于图像处理和计算机图形学中的相似性检测。

总结

全等三角形是一种具有特殊性质的三角形，它的定义、性质和判定方法都非常重要。了解全等三角形的定义和性质，可以帮助我们更好地理解和应用全等三角形在各个领域中的应用。

同时，掌握全等三角形的判定方法，可以提高我们在解决实际问题时的效率和准确性。

以上分享的全等三角形的定义，性质，判定的相关内容，希望对您有所帮助！