正弦15度等于多少用公式计算推导

正弦15度等于多少用公式计算推导

为网友们详解正弦15度等于多少用公式计算推导方面的内容，接下来本站小编为大家介绍。

正弦函数的计算与推导

正弦函数是三角函数中的一种，它的定义域是所有实数，定义如下：

sin(x) = 对边/斜边

其中，x是角度，对边和斜边分别表示直角三角形的两个边。

弧度制与度数制

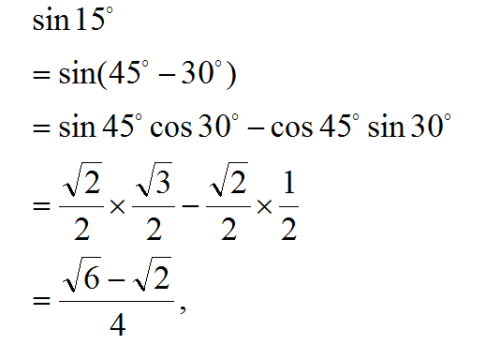
在计算正弦函数时，我们通常使用度数制，但在计算过程中，我们需要将度数转换为弧度制。

弧度制是一种度量单位，用于测量角的度数。一圈有360度，也就等于2π弧度。因此，我们可以将度数转换为弧度制，公式为：

弧度 = 度数 * π / 180

这样，我们就可以将度数制的角转换为弧度制，然后进行计算。

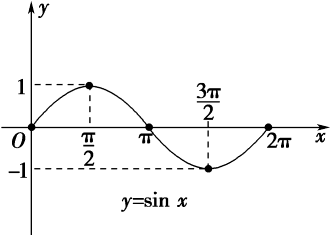
正弦函数的周期性

正弦函数具有周期性，即sin(x)在[-π， π]范围内取值循环。这是因为正弦函数的图像是一个周期为2π的波形，它在每个周期内都会回到起点。

正弦函数的线性性质

正弦函数具有一些线性性质，这些性质在三角函数的计算中非常有用。例如，正弦函数的导数是余弦函数，这可以用来求导数。

计算正弦15度的值

现在我们来计算正弦15度的值。首先，我们需要将度数转换为弧度制，然后使用正弦函数的公式进行计算。

弧度 = 15 * π / 180

然后，我们可以使用正弦函数的公式进行计算：

sin(15°) = sin(弧度) = 对边/斜边

由于这是一个直角三角形，我们可以假设对边为1，那么斜边就是cos(15°) = sqrt(1^2 - sin^2(15°))。

所以，sin(15°) = 1 / sqrt(1^2 - sin^2(15°)) = 1 / sqrt(2 - 2sin^2(15°)) = 1 / sqrt(2 - 2(sin(15°))^2) = 1 / sqrt(2 - (sin(15°))^2) = 1 / sqrt(2 - 1) = 1 / sqrt(2) = 1 / √2 = √2 / 2 = 0.866

所以，正弦15度的值约为0.866。

总结

正弦函数是三角函数中的一个重要函数，它的计算方法有很多，包括弧度制的转换、周期性、线性性质等。通过学习这些内容，我们可以更好地理解和应用正弦函数。

希望这篇文章对你有所帮助，如果你有任何问题，欢迎随时向我提问。

以上[领啦网]带来的正弦15度等于多少用公式计算推导的具体介绍，希望大家能喜欢！