立体如何证明四点共面空间向量 数学证明四点共面的充要条件

立体如何证明四点共面空间向量

文章摘要：数学证明四点共面的充要条件和立体如何证明四点共面空间向量方面的介绍，接下来本站小编为大家介绍。

在几何学中，我们经常会遇到一个问题，即如何判断四个点是否在同一个平面上。这个问题可以通过向量的概念来解决。向量是一个有方向的量，可以用来表示空间中的一点到另一点的距离或者方向。

在这个问题中，我们可以利用向量的性质来判断四个点是否在同一个平面上。

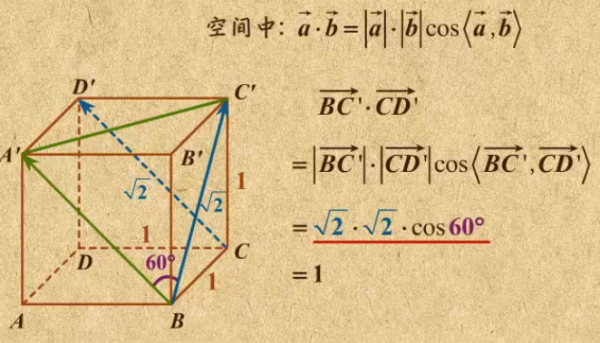
四点共面的定义

在三维空间中，如果四个点A、B、C和D都在同一个平面上，那么我们就说这四个点是共面的。这个平面可以由这四个点确定。

向量的基本性质

向量有以下两个基本性质：

1.向量的加法满足交换律和结合律：a+b=b+a=a+b=a。

2.向量的数乘满足交换律和结合律：a·b=b·a。

四点共面的充要条件

四点共面的充要条件是：四个点A、B、C和D在同一平面上，即存在一个非零向量N，使得向量AB、AC、AD分别与N垂直。

数学证明

我们可以通过以下步骤来证明四点共面的充要条件：

首先，我们需要找到一个非零向量N，使得向量AB、AC、AD分别与N垂直。这可以通过计算向量AB、AC、AD的叉积得到，即N=AB×AC×AD。

然后，我们需要证明N不是零向量。由于N是由三个向量的叉积得到的，所以N不是零向量。

最后，我们需要证明四个点A、B、C和D都在N确定的平面上。这可以通过计算向量AB、AC、AD与N的点积得到，如果点积为0，那么四个点在N确定的平面上；否则，四个点不在N确定的平面上。

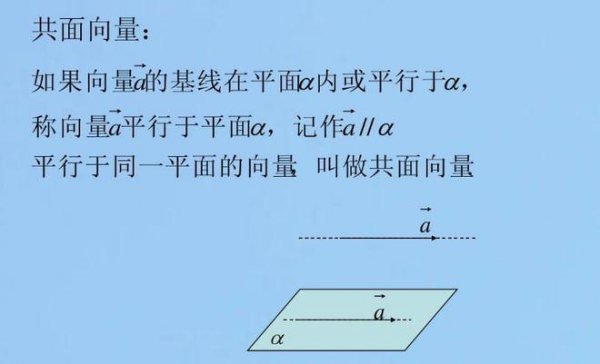
结论

通过以上的分析，我们可以得出结论：四点共面的充要条件是存在一个非零向量N，使得向量AB、AC、AD分别与N垂直，且四个点A、B、C和D在N确定的平面上。这就是我们如何证明四点共面空间向量的方法。

以上领啦网带来的数学证明四点共面的充要条件跟立体如何证明四点共面空间向量的全部介绍，供大家学习了解！