二次函数因式分解法的四种方法及例题

二次函数因式分解法的四种方法及例题

本文为你详解二次函数因式分解法的四种方法及例题方面的内容，如有不对的地方欢迎指正！

二次函数是初中数学中的一个重要内容，它在实际生活中有着广泛的应用。

在解决二次函数问题时，因式分解法是一种常用的方法。本文将介绍二次函数因式分解法的四种方法及例题，帮助同学们更好地理解和掌握这一知识点。

一、完全平方公式法

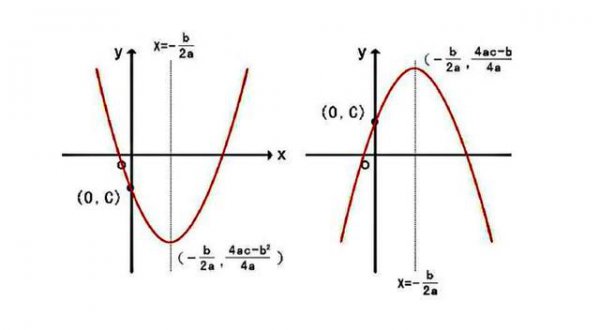
完全平方公式法是指将二次函数写成一个完全平方的形式，然后进行因式分解。这种方法适用于形如ax²+bx+c=0（a≠0）的二次函数。

例1：求解方程x²-3x-4=0。

解：将方程改写为x²-3x=4，然后利用完全平方公式法进行因式分解，得到（x-4）（x+1）=0，所以x₁=4，x₂=-1。

二、十字相乘法

十字相乘法是指将二次函数的二次项和常数项分别分解成两个因数，然后将这两个因数相乘，得到一个新的二次函数。这种方法适用于形如ax²+bx+c=0（a≠0）的二次函数。

例2：求解方程x²-5x+6=0。

解：将方程改写为x²-5x=-6，然后利用十字相乘法进行因式分解，得到（x-6）（x+1）=0，所以x₁=6，x₂=-1。

三、双十字相乘法

双十字相乘法是指在十字相乘法的基础上，再对一次项进行因式分解。这种方法适用于形如ax²+bx+c=0（a≠0）的二次函数。

例3：求解方程x²-7x+12=0。

解：将方程改写为x²-7x=-12，然后利用双十字相乘法进行因式分解，得到（x-3）（x-4）=0，所以x₁=3，x₂=4。

四、分组分解法

分组分解法是指将二次函数的二次项和常数项分成两组，然后分别进行因式分解。这种方法适用于形如ax²+bx+c=0（a≠0）的二次函数。

例4：求解方程x²-9x+8=0。

解：将方程改写为（x-8）（x-1）=0，所以x₁=8，x₂=1。

通过以上四个例题，我们可以看到二次函数因式分解法的应用非常广泛。在解决实际问题时，我们需要根据具体问题选择合适的方法进行因式分解。同时，我们还需要注意以下几点：

1. 在进行因式分解时，要注意保持等式的平衡，即左边的因式等于右边的常数项。

2. 在进行因式分解时，要注意检查是否有重复的因式，如果有，需要将其合并。

3. 在进行因式分解时，要注意检查是否有互为相反数的因式，如果有，需要将其合并。

总之，二次函数因式分解法是解决二次函数问题的重要方法之一。掌握这四种方法及其应用，对于提高我们的数学素养和解决实际问题具有重要意义。

希望同学们在学习过程中，能够认真思考，多加练习，不断提高自己的解题能力。

上述的关于二次函数因式分解法的四种方法及例题的具体内容，未经「领啦网」[www.lingla.com]允许禁止转载！