空间向量的模的计算公式理解与推导

空间向量的模的计算公式理解与推导

『领啦网』小编为你介绍空间向量的模的计算公式理解与推导的相关话题，接下来本站小编为大家介绍。

空间向量的模是描述向量大小的一个重要概念，它在几何、物理等领域有着广泛的应用。本文将对空间向量的模的计算公式进行理解和推导，帮助读者更好地掌握这一知识点。

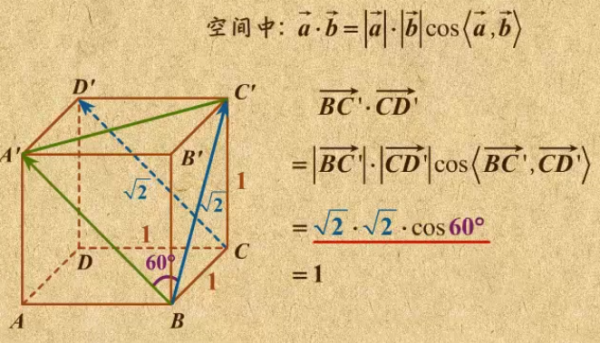
首先，我们需要了解什么是空间向量。在三维空间中，任意两个不共线的向量都可以构成一个平面。这个平面上的任意一点都可以表示为这两个向量的线性组合，即：

P = a * A + b * B

其中，P 是空间中的一个点，A 和 B 是两个不共线的向量，a 和 b 是实数。这个公式表明，空间中的任何一个点都可以用两个不共线的向量来表示。这种表示方法被称为空间向量的基底表示法。

接下来，我们来介绍空间向量的模的定义。空间向量的模是一个非负实数，它表示了向量的大小。具体来说，向量 A 的模定义为：

||A|| = (A·A)^(1/2)

其中，A·B 表示向量 A 和 B 的点积，即：

A·B = |A||B|cosθ

其中，θ 是向量 A 和 B 之间的夹角。从这个定义可以看出，向量的模实际上就是向量与其自身的点积的平方根。

现在，我们来推导空间向量的模的计算公式。根据空间向量的基底表示法，我们可以将任意一个空间向量表示为两个不共线的向量的线性组合。设向量 P 可以表示为：

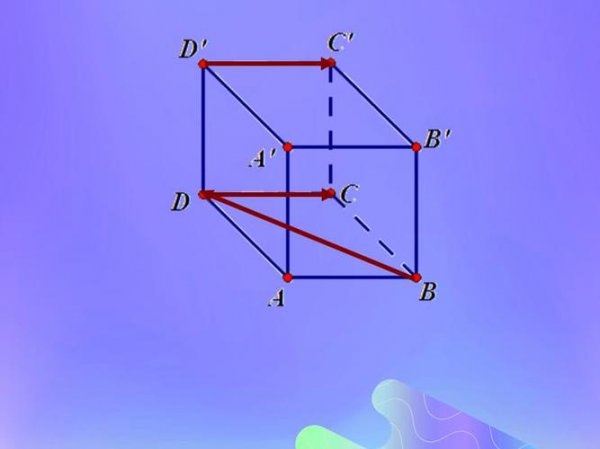
P = a * A + b * B

其中，a 和 b 是实数。那么，向量 P 的模可以表示为：

||P|| = ||a * A + b * B|| = ||a*A|| + ||b*B||

其中，||·|| 表示向量的模。由于 A 和 B 是不共线的向量，所以它们之间的夹角不为0。因此，我们可以将上式进一步化简为：

||P|| = ||a*A||^2 + ||b*B||^2 + 2ab*A·B

接下来，我们来计算上式中的每一项。首先计算 ||a*A||^2：

||a*A||^2 = (a*A·a*A)^(1/2) = (a^2*A·A)^(1/2) = a^2*||A||^2

同理，我们可以计算出 ||b*B||^2 = b^2*||B||^2。最后，我们来计算 2ab*A·B：

2ab*A·B = 2ab*|A||B|cosθ = 2ab*|A||B|cosθ

将上述结果代入原式，得到：

||P|| = a^2*||A||^2 + b^2*||B||^2 + 2ab*|A||B|cosθ

这就是空间向量的模的计算公式。通过这个公式，我们可以方便地计算出任意一个空间向量的模。需要注意的是，这个公式只适用于不共线的向量。如果两个向量共线，那么它们的模都是0。

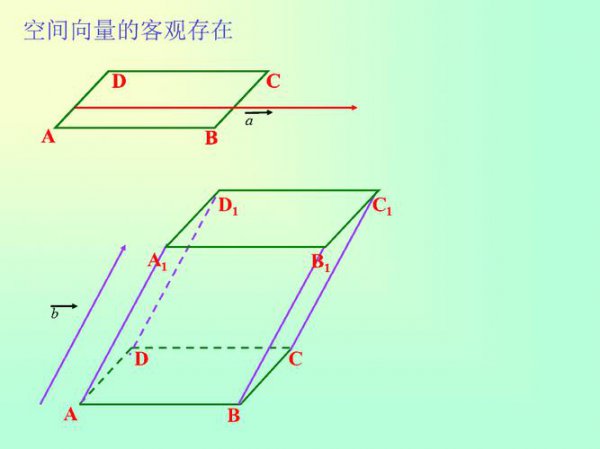
总之，空间向量的模是一个描述向量大小的重要概念。通过理解其定义和推导过程，我们可以更好地掌握这一知识点。

在实际应用中，空间向量的模有着广泛的应用，如计算距离、判断方向等。希望本文能帮助读者更好地理解和应用空间向量的模。

上面(『领啦网』)为您介绍的空间向量的模的计算公式理解与推导的具体介绍，希望给网友们带来一些知识。