双曲线焦点到渐近线的距离等于多少怎么计算

双曲线焦点到渐近线的距离等于多少怎么计算

小编为大家说一说双曲线焦点到渐近线的距离等于多少怎么计算方面的介绍，接下来「领啦网」小编为大家介绍。

一、引言

双曲线是数学中的一种重要图形，它在物理、工程、经济等多个领域都有广泛的应用。在双曲线的研究中，焦点到渐近线的距离是一个非常重要的概念，它涉及到双曲线的性质和特征。

本文将详细介绍如何计算双曲线焦点到渐近线的距离。

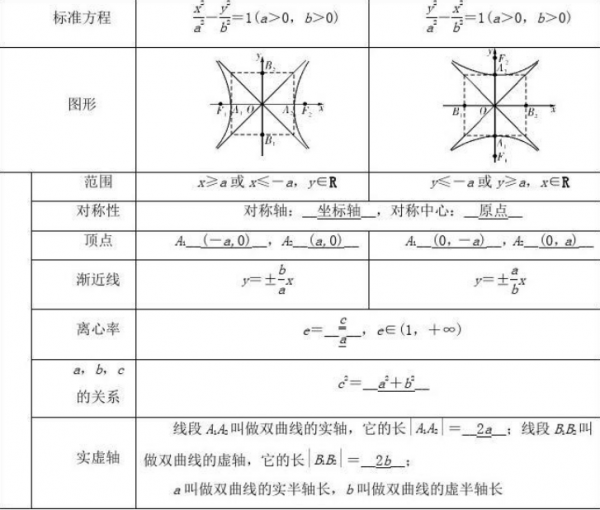
二、双曲线的基本概念

双曲线是由两个相交的直线和一个不在这两直线上的点组成的图形。这两个相交的直线被称为渐近线，而那个不在这两直线上的点被称为焦点。

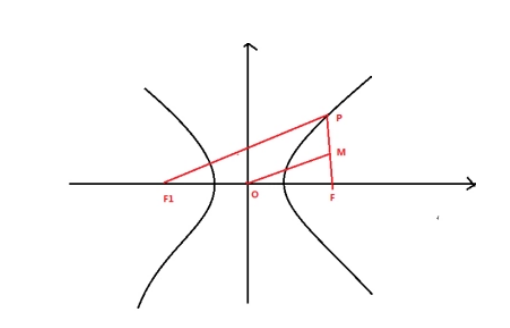
双曲线的焦点到渐近线的距离是指从焦点到任一条渐近线的最短距离。

三、双曲线的性质

双曲线有两个重要的性质，一是它的焦点到渐近线的距离是固定的，二是这个距离与双曲线的尺度无关。这两个性质为我们计算双曲线焦点到渐近线的距离提供了便利。

四、双曲线焦点到渐近线的距离的计算方法

计算双曲线焦点到渐近线的距离，我们可以采用以下步骤：

1. 确定双曲线的方程

双曲线的一般方程为Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0.其中A, B, C, D, E, F为常数。

2. 确定双曲线的焦点和渐近线

双曲线的焦点可以通过求解方程Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0得到，而渐近线可以通过求解方程Bx + Cy = 0得到。

3. 计算焦点到渐近线的距离

根据勾股定理，我们可以计算出焦点到渐近线的距离。

具体来说，如果我们选择焦点F(c, 0)和渐近线L：Bx + Cy = 0.那么焦点到渐近线的距离d可以通过以下公式计算：d = |F(c, 0) - L| / sqrt(B^2 + C^2)。

五、实例分析

为了更直观地展示如何计算双曲线焦点到渐近线的距离，我们来看一个实例。

假设我们有一个双曲线，其方程为4x^2 - 5y^2 = 4.其焦点为（1.0）和（-1.0），其渐近线为y = sqrt(4/5)x和y = -sqrt(4/5)x。

那么，焦点到渐近线的距离可以通过以下步骤计算：

1. 首先，我们确定双曲线的方程为4x^2 - 5y^2 = 4.

2. 然后，我们确定双曲线的焦点为(1.0)和(-1.0)，渐近线为y = sqrt(4/5)x和y = -sqrt(4/5)x。

3. 最后，我们计算焦点到渐近线的距离。由于焦点F（1.0）到渐近线y = sqrt（4/5）x的距离为|F（1.0） - L| / sqrt(4/5 + (-5)^2) = |1*sqrt(4/5) - 0| / sqrt(4/5 + 25) = 1/7.所以焦点到渐近线的距离为1/7.

六、结论

通过以上分析，我们可以看到，计算双曲线焦点到渐近线的距离并不复杂，只需要按照一定的步骤进行即可。

然而，这个过程中需要注意的是，我们需要先确定双曲线的方程，然后确定双曲线的焦点和渐近线，最后才能计算出焦点到渐近线的距离。

此外，我们还需要注意，双曲线的焦点到渐近线的距离是固定的，与双曲线的尺度无关。

以上分享的双曲线焦点到渐近线的距离等于多少怎么计算的全文内容了希望能帮助到您，同时也希望大家多来[「领啦网」]看看更多的生活经验常识！