一次函数的定义和性质 一次函数的定义域和值域单调性

一次函数的定义和性质

为关注「领啦网」的网友们详解一次函数的定义和性质方面的知识，一定能给您带来帮助的，一起来了解吧！

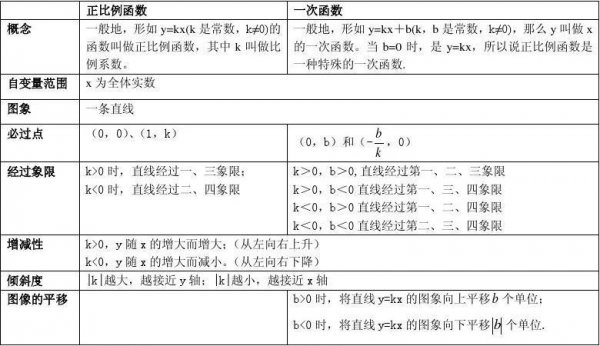
一次函数是数学中最简单的函数之一。它的定义是一个常数与自变量的一次幂相乘再加上一个常数，表示为y=ax+b。其中，a表示斜率，b表示截距，x和y分别表示自变量和因变量。

一次函数通常用来描述线性关系，如距离和时间、温度和时间等。

一次函数的性质

一次函数的性质主要有三点：

一次函数的定义域和值域

一次函数的定义域是所有可输入函数的自变量的值的集合。根据一次函数的定义，x可以取任何实数的值，因此一次函数的定义域为实数集。

其次，一次函数的值域是所有可输出函数的因变量的值的集合。因为y=ax+b在实数集中可以取到任何实数的值，所以一次函数的值域也是实数集。

一次函数的单调性

一次函数的单调性是指函数图像沿着x轴的正方向或者负方向运动时，函数值的变化趋势。

根据一次函数的定义，当斜率a为正数时，函数是递增的，当a为负数时，函数是递减的。

而截距b不影响函数的单调性。所以我们可以得出一次函数的单调性与a的正负有关。

一次函数的图像

一次函数的图像是一条直线。斜率a决定了直线的倾斜程度，而截距b决定了直线与y轴的交点位置。

当a为正数时，直线向上倾斜；当a为负数时，直线向下倾斜。当b为正数时，交点在y轴上方；当b为负数时，交点在y轴下方。一个典型的一次函数图像如下：


应用举例

一次函数可以应用于很多实际问题中。比如，我们可以用一次函数来描述一个物体经过一段时间后的位移、速度或加速度变化。具体应用举例如下：

位移问题

举例：一辆汽车从静止开始匀加速行驶，10秒后速度达到20m/s，求此时汽车的位移。

解析：根据运动学公式，已知时间、初速度和加速度可以求出位移。有v = at，变形得a = v/t = 20m/s ÷ 10s = 2m/s2。

设t秒后汽车行驶的位移为S，则有S = (1/2)at2= (1/2) × 2m/s2 × (10s)2 = 100m。经过10秒后，汽车行驶的位移是100米。

我们可以用一次函数来表示汽车行驶的距离S和时间t的关系。设S为函数值，t为自变量，则有S = at2/2。根据定义，斜率a = v/t = 2m/s2，截距b = 0。所以该函数可以表示为S = 2t2。

速度问题

举例：一辆汽车从静止开始匀加速行驶，10秒后速度达到20m/s，求此时汽车的速度。

解析：根据运动学公式，已知时间、初速度和加速度可以求出速度。有v = at，变形得a = v/t = 20m/s ÷ 10s = 2m/s2。

设t秒后汽车的速度为v，则有v = at = 2m/s2 × 10s = 20m/s。经过10秒后，汽车的速度是20米/秒。

我们可以用一次函数来表示汽车的速度v和时间t的关系。设v为函数值，t为自变量，则有v = at。根据定义，斜率a = 2m/s2，截距b = 0。所以该函数可以表示为v = 2t。

加速度问题

举例：一辆汽车从静止开始匀加速行驶，10秒后速度达到20m/s，求此时汽车的加速度。

解析：根据运动学公式，已知时间、初速度和加速度可以求出加速度。有v = at，变形得a = v/t = 20m/s ÷ 10s = 2m/s2。经过10秒后，汽车的加速度是2米/秒2。

我们可以用一次函数来表示汽车的加速度a和时间t的关系。

设a为函数值，t为自变量，则有a = v/t = 2m/s2。根据定义，斜率a = 0，截距b = 2。所以该函数可以表示为a = 2。

一次函数是最简单的函数之一，通常用于描述线性关系。

一次函数的定义域和值域都为实数集，而其单调性与斜率a的正负有关。一次函数的图像是一条直线，斜率和截距分别对应线段的倾斜程度和与y轴的交点。

一次函数在实际问题中有广泛的应用，如描述物体的位移、速度和加速度变化等。

以上分享的一次函数的定义域和值域单调性和一次函数的定义和性质的详细讲解，仅供大家参考建议！