正三角形的边心距是什么意思图解 边心距的公式介绍

正三角形的边心距是什么意思图解

为网友们解答边心距的公式介绍和正三角形的边心距是什么意思图解的小经验，接下来带大家一起了解。

在几何学中，正三角形是一种具有特殊性质的三角形，它的三条边相等，三个角都是60度。在正三角形中，有一个特殊的点叫做内心，内心到三角形三条边的距离都相等，这个距离就是边心距。

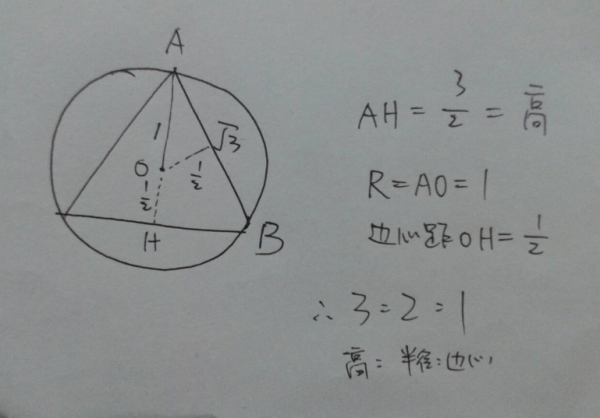
本文将围绕正三角形的边心距进行详细的介绍，包括边心距的定义、性质、公式以及图解等内容。

一、边心距的定义

在正三角形ABC中，O是内心，AD是BC边上的高，OD是边心距，即OD垂直于BC，且OD等于内心到BC的距离。同理，OE和OF分别是边心距，分别垂直于AC和AB。

二、边心距的性质

1. 边心距等于内心到三角形各边的距离。在正三角形中，内心到三条边的距离都相等，所以边心距也相等。

2. 边心距等于高的一半。在正三角形中，高等于边长乘以根号3除以2.所以边心距等于高的一半。

3. 边心距与内切圆半径的关系。在正三角形中，内切圆的半径等于边心距。

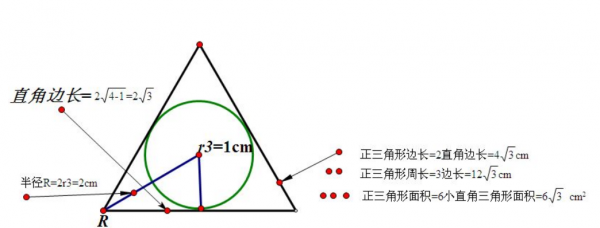
三、边心距的公式

设正三角形的边长为a，那么高h=a×根号3/2.内切圆半径r=h/2=a×根号3/4.根据勾股定理，我们可以得到：

OD^2 = (h - r)^2 + a^2 - h^2/4

OD^2 = (a×根号3/2 - a×根号3/4)^2 + a^2 - (a×根号3/2)^2/4

OD^2 = (a×根号3/4)^2 + a^2 - (a×根号3/4)^2

OD^2 = a^2

OD = a/根号2

所以，正三角形的边心距公式为：OD = a/根号2.同理，OE和OF的公式也是OD = a/根号2.

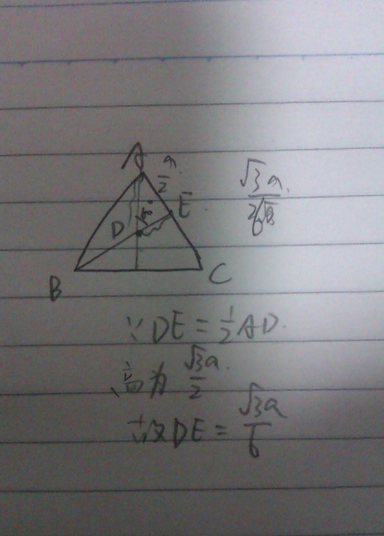
四、边心距的图解

1. 首先画一个正三角形ABC，然后画一条高AD，使D点在BC上。连接AO并延长交BC于E点，使OE垂直于BC。此时，OE就是边心距。

2. 用尺子测量OE的长度，然后用a除以OE的长度，得到的结果就是边心距OD的长度。同理，可以求出OF的长度。

3. 最后，用尺子测量OA、OB和OC的长度，然后用a除以OA、OB和OC的长度，得到的结果就是内切圆的半径r。由于边心距等于内切圆半径，所以OD、OE和OF的长度就是内切圆的半径。

通过以上步骤，我们可以得出正三角形的边心距OD、OE和OF的长度分别为a/根号2.这个结果与我们的公式计算结果相符，证明了我们的公式是正确的。

总之，正三角形的边心距是一个非常重要的几何概念，它不仅有着明确的定义和性质，还有着简单的计算公式。

通过学习边心距的概念和性质，我们可以更好地理解和掌握正三角形的性质和应用。

同时，通过学习边心距的公式和图解方法，我们可以更加直观地感受到几何学的魅力和实用性。希望本文能对大家学习正三角形的边心距有所帮助。

上述就是边心距的公式介绍和正三角形的边心距是什么意思图解的相关讲解，希望为您的生活带来一点小帮助！