牟合方盖指的是什么 牟合方盖是是谁提出并计算的(4)

牟合方盖指的是什么

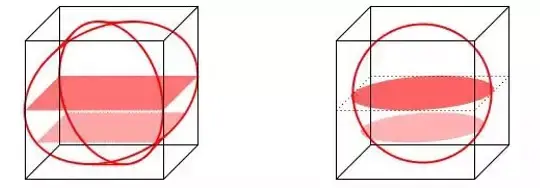
因此，刘徽发现，牟合方盖的体积与相应内切球的体积之比也应是4：π，到这里，实际上已经接近了积分学中以意大利数学家命名的“卡瓦列里定理”，可惜的是，他没能算出牟合方盖的体积，以至于最终没能得出球的体积公式。

☆ 牟合方盖的体积

在大概160年以后，祖氏父子横空出世，提出"幂势既同则积不容异"，即等高的两立体，若其任意高处的水平截面积相等，则这两立体体积相等，这就是著名的祖暅原理。

祖冲之更厉害，不仅首次把π精确到小数点后第7位（祖率），并且保持该项世界纪录近1000年。

祖氏利用祖暅原理，最终算出牟合方盖的体积，并最终得到球的体积公式。

当然，更厉害的人物是阿基米德，他早于刘徽大约500年就得出球的体积公式，也得出π=3.14。言归正传，下面是牟合方盖的体积计算方法：

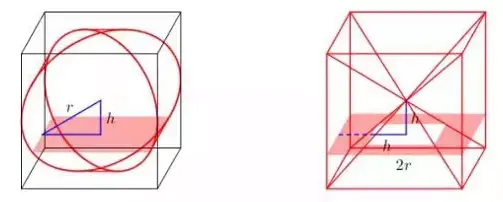
上面右图是一个正方体挖去了两个四棱锥（这两个四棱锥分别以上下底面为底面，以正方体的中心为顶点），设正方体边长为2r。以平行于底面的平面同时截“牟合方盖”和“右图的几何体”，所得截面如上图所示。

左图的截面是一个正方形，设中心到截面的距离为h，可得该正方形边长为2√r²-h²，所以左图的截面面积为4（r²-h²）

右图的截面像一个正方环形，面积是大正方形的面积减去小正方形的面积，边长为2r，所以大正方形面积为4r²，同样设中心到截面的距离为h，可知小正方形的边长为2h，所以小正方形的面积为4h²，即截面面积为4r²-4h²。

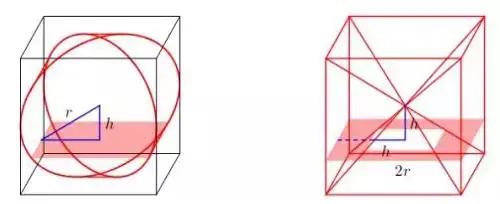
由上可知，两几何体在同一水平位置的截面面积相等，根据祖暅原理，它们的体积相等，右图的体积等于正方体的体积减去两个四棱锥的体积。

根据锥的体积公式可知，两个锥的体积之和为正方体体积的1/3，所以该几何体的体积为正方体体积的2/3，即“牟合方盖”的体积为正方体体积的2/3，正方体体积为8r³，所以最终，“牟合方盖”的体积为16r³/3。

结合刘徽得出的结论，“牟合方盖”的体积与内切球的体积之比为4：π，由此得出，球的体积为4πr³/3。

☆ 结语

“牟合方盖”的提出，充分体现了古人丰富的想象能力，以及为解决问题建立模型的智慧。祖氏父子应用这个原理，解决了刘徽尚未解决的球体积公式。

该原理在西方直到十七世纪才由意大利数学家卡瓦列利(BonaventuraCavalier)发现，比祖暅晚一千一百多年。

刘徽是1700多年前的人，祖氏父子是1500多年前的人，阿基米德更是2200年前的人，以千年前的社会知识水平，就在思考这种问题，简直令人叹为观止，这种智慧的光芒，震古烁今，光耀寰宇。

以上[领啦网]带来的牟合方盖是是谁提出并计算的及其牟合方盖指的是什么的全文内容，希望对网友有所帮助！