怎么证明平行四边形判定方法 对角相等如何证明平行四边形
怎么证明平行四边形判定方法
本文为你介绍对角相等如何证明平行四边形和怎么证明平行四边形判定方法的相关话题,接下来带大家一起了解。
平行四边形是几何学中的一种基本图形,它有两对对边分别平行且相等。在证明一个四边形为平行四边形时,我们通常使用以下几种方法:对角线法、对角互补法、同旁内角互补法等。
本文将重点介绍如何证明平行四边形判定方法中的“对角相等”这一条件。
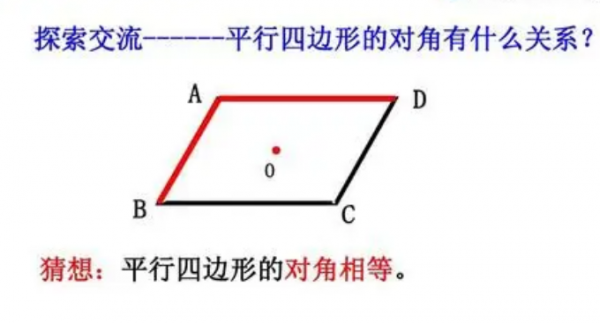
首先,我们需要明确什么是对角相等。在平行四边形中,相对的两条边的夹角称为对角。当一个四边形的两组对角分别相等时,我们称这个四边形为平行四边形。
换句话说,如果一个四边形的四个内角之和等于360度,且相邻两个内角之和等于180度,那么这个四边形就是平行四边形。

接下来,我们将通过几个步骤来证明一个四边形满足对角相等的条件时,它是平行四边形。
步骤一:
已知四边形ABCD中,∠A与∠C相等,∠B与∠D相等。我们需要证明四边形ABCD是平行四边形。
步骤二:
由于∠A与∠C相等,我们可以得出∠A + ∠C = 180°。同样地,由于∠B与∠D相等,我们可以得出∠B + ∠D = 180°。
步骤三:
由于四边形的四个内角之和等于360°,我们可以得出2 × (∠A + ∠C) + 2 × (∠B + ∠D) = 360°。将步骤二中的结论代入上式,得到2 × 180° + 2 × 180° = 360°,即360° = 360°。这说明我们的假设是正确的,即四边形ABCD的四个内角之和确实等于360°。
步骤四:由于四边形的相邻两个内角之和等于180°,我们可以得出∠A + ∠B = 180°,∠C + ∠D = 180°。将步骤二中的结论代入上式,得到∠A + ∠B = 180°,∠C + ∠D = 180°。这说明四边形ABCD的两组对角分别相等。
步骤五:根据平行四边形的定义,当一个四边形的两组对角分别相等时,它就是平行四边形。因此,我们可以得出结论:四边形ABCD是平行四边形。
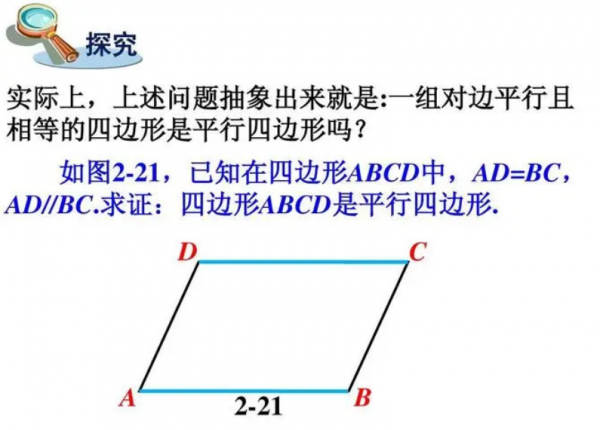
通过以上五个步骤,我们证明了当一个四边形满足对角相等的条件时,它是平行四边形。这种方法在实际问题中的应用非常广泛,例如在解决几何题、分析图形性质等方面都有很大的帮助。
总之,对角相等是证明平行四边形的一个关键条件。通过熟练掌握这一方法,我们可以更加轻松地判断一个四边形是否为平行四边形,从而更好地解决各种几何问题。希望本文能对你有所帮助,祝你在学习几何学的道路上越走越远!
以上分享的对角相等如何证明平行四边形以及怎么证明平行四边形判定方法的详细讲解,希望本文能给你带来生活上的帮助!