奇函数乘以偶函数等于什么函数 函数知识点总结

奇函数乘以偶函数等于什么函数

全面为您解析函数知识点总结和奇函数乘以偶函数等于什么函数的相关话题，相关内容具体如下：

在数学中，函数是一种基本的数学概念，它是一种特殊的关系，描述了两个变量之间的依赖关系。函数的基本形式是y=f(x)，其中y是因变量，x是自变量。

根据函数的性质，我们可以将函数分为奇函数和偶函数。那么，当奇函数乘以偶函数时，结果会是什么函数呢?这是我们今天要探讨的问题。

首先，我们需要明确什么是奇函数和偶函数。

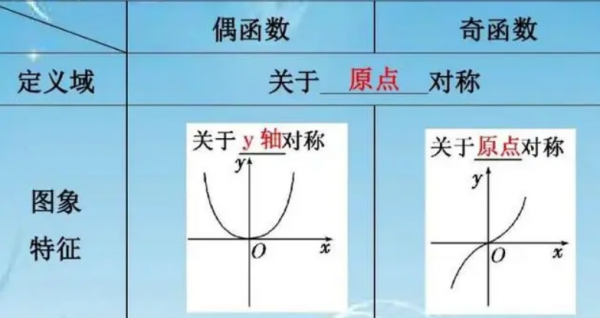
奇函数是指满足f(-x)=-f(x)的函数，即对于任何实数x，都有f(-x)=-f(x)。奇函数的图像关于原点对称。例如，f(x)=-x就是奇函数。

偶函数是指满足f(-x)=f(x)的函数，即对于任何实数x，都有f(-x)=f(x)。偶函数的图像关于y轴对称。例如，f(x)=x^2就是偶函数。

那么，奇函数乘以偶函数会是什么呢?

根据乘法分配律，我们知道，一个奇函数和一个偶函数的乘积仍然是奇函数。这是因为，奇函数f(-x)=-f(x)和偶函数f(-x)=f(x)的乘积为[f(-x)]*[f(-x)]=-[f(x)]*[f(x)]=-f(x)*f(x)=-[f(-x)]*[f(-x)]，这正好满足了奇函数的定义。

因此，我们可以得出结论：奇函数乘以偶函数等于奇函数。

这个结论在我们的实际生活中有很多应用。例如，在电磁学中，交流电的振幅和相位就可以看作是一个奇函数和一个偶函数的乘积，因此它们的乘积仍然是一个奇函数，这就解释了为什么交流电的振幅和相位的乘积是一个常数的原因。

此外，这个结论也可以帮助我们更好地理解和掌握函数的性质。通过研究奇函数和偶函数的性质，我们可以更好地理解函数的图像、性质和应用。

例如，我们可以通过研究奇函数和偶函数的图像，来了解它们的特点和规律;我们也可以通过研究奇函数和偶函数的性质，来了解它们在数学和物理中的应用。

总的来说，奇函数乘以偶函数等于奇函数，这是一个非常重要的数学结论。

它不仅可以帮助我们解决实际问题，也可以帮助我们更好地理解和掌握函数的性质。因此，我们应该深入理解和掌握这个结论，以便在学习和工作中更好地应用它。

以上就是函数知识点总结以及奇函数乘以偶函数等于什么函数的具体介绍，希望大家能喜欢！