π是有理数还是无理数 人们终于证明了π是无理数(2)
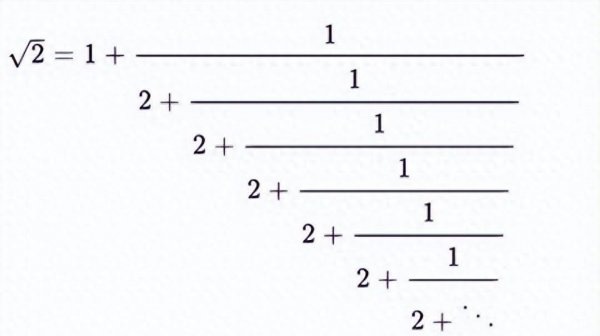
导读:π是有理数还是无理数,黄金分割数(√5-1)/2的无限连分数很有意思: 黄金分割数无限连分数 1761年,瑞士数学家兰伯特受此启发,历史上第一次给出了π是无理数的严格证明。 他
π是有理数还是无理数
黄金分割数(√5-1)/2的无限连分数很有意思:
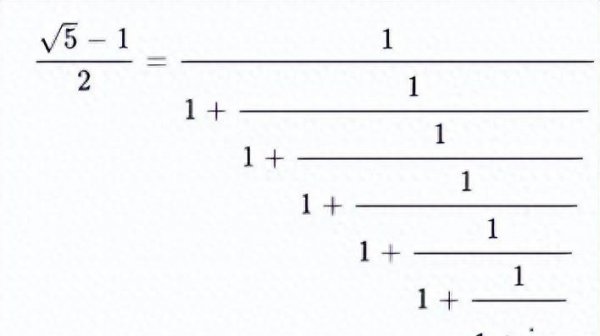
黄金分割数无限连分数
1761年,瑞士数学家兰伯特受此启发,历史上第一次给出了π是无理数的严格证明。
他首先证明了正切函数tan(x)可以表示成类似无限连分数的无限连分函数形式:
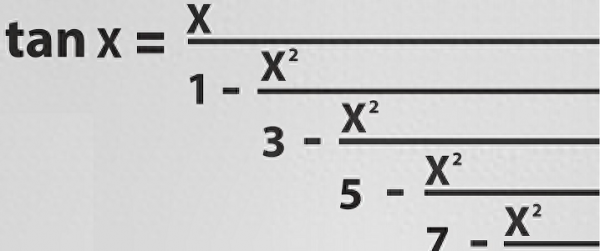
利用以上结论,兰伯特进而证明了:如果x是非0有理数,那么tan(x)必然是无理数。这个结论非常有意思,证明过程有些繁杂,这里略去不讲,有兴趣的朋友可以进一步了解一下。
特别注意:这个结论只说了“如果x是非0有理数,那么tan(x)必然是无理数”;并没有说“如果x是无理数,那么tan(x)必然是有理数”。这里一定要区分开来。
有了以上基础理论,接下来我们就可以利用反证法来证明π是无理数了。
求证:π是无理数
证明:假设π是有理数
显然π/4也是有理数,且π/4≠0
我们有结论:如果x是非0有理数,那么tan(x)必然是无理数
所以tan(π/4)是无理数
tan(π/4)=tan(45°)=1是有理数
与tan(π/4)是无理数矛盾
说明假设“π是有理数”错误
所以π是无理数
证毕!
这个证明过程简洁清晰、逻辑缜密,堪称反证法应用的经典例证,真是让人赏心悦目。
至此,人们终于严格证明了π是无理数,后来人们还采用了构造函数、微积分等多种方法证明了π是无理数。但相比而言,兰伯特给出的证明方法更加符合数学的极致美学。
以上[领啦网]介绍的人们终于证明了π是无理数和π是有理数还是无理数的全部介绍了希望能给您带来帮助,最后别忘了多来[领啦网]瞧一瞧更多的经验常识!
上一篇:四川广元是几线城市2023
下一篇:手相有科学依据吗 手相这东西准吗