π是有理数还是无理数 人们终于证明了π是无理数

π是有理数还是无理数

本文为你介绍人们终于证明了π是无理数和π是有理数还是无理数的内容，如有不对的地方欢迎指正！

我们都知道圆周率π，π的定义是一个圆的周长和这个圆的直径的比值。

π=圆周长：直径

圆周长=直径×π=2R×π=2πR

我国古代著名数学家祖冲之利用割圆术将π精确计算到小数点后第7位，这种精度领先西方数学500多年。

3.1415926＜π＜3.1415927

大约在2000多年前，人们就已经发现了圆周率π。从直觉上来看，π显然应该是一个无理数，也就是一个无限不循环小数。

但直觉是不靠谱的，我们必须严格证明才能真正地让所有人信服。为了严格证明π是无理数人类用了整整2000多年的时间！

接下来我们就来探讨一下如何严格证明π是无理数。

首先我们需要了解在实数范围内，除了有理数就是无理数。也就是说，有理数集Q和无理数集的交集是空集∅，并集是实数集R。

有理数是指有限小数或无限循环小数，这里将整数视为有限小数。所有的有理数都可以写成既约整分数的形式，这里将整数视为分母为1的分数。所谓既约整分数就是指分子分母都是整数并且约到最简的分数。

若a∈Q，则a=m/n，这里m、n∈整数集z，且(m，n)=1，n≠0。这里符号(m，n)，代表正整数m和n的最大公约数，若(m，n)=1，则称m和n互质。

无理数是指无限不循环小数，任何无理数都不能写成两个整数相除的分数形式。

接下来我们介绍连分数的概念。

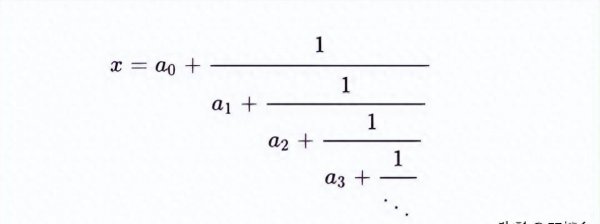
我们把形如上图形式的分数称为连分数，这里a0，a1，a2，a3，……，都是整数。

可以证明任何一个有理数都对应某一个有限连分数，任何一个无理数都对应某一个无限连分数。这里证明从略。

例如有理数3.245的有限连分数如下：

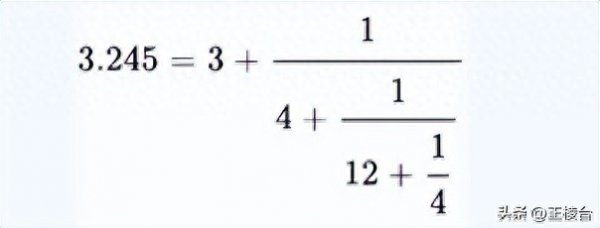
有理数有限连分数

无理数√2的无限连分数如下：