三角形的内角和是多少少度？一定是 180°吗？(2)

三角形的内角和是多少少度？一定是

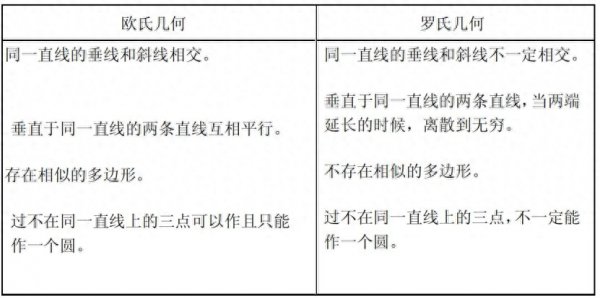
机智的你可能已经发现，上面这些命题和我们的直觉是矛盾的。

但是，数学家们经过思考提出，可以用我们习惯的办法作一个直观“模型”来证实它的正确性。

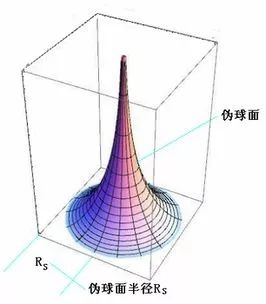
1868 年，意大利数学家贝特拉米发表了一篇著名论文 《非欧几何解释的尝试》 ，证明 非欧几何学可以在欧几里得空间的曲面（例如拟球曲面）上实现。

他发现 这里三角形的三个内角之和小于180° ，这相当于给罗氏几何找到了一种有实际意义的模型。

那个时代被誉为“ 数学王子 ”的高斯也发现了第五公设不能被证明，同时也涉足了非欧几何学的研究。

但高斯害怕这种理论会遭到当时教会力量的打击和迫害，不敢公开发表自己的研究成果，只是在书信中向朋友表示了自己的看法，并没有公开支持罗巴切夫斯基的新理论。

黎曼几何学

那么既然我们能把第五公里改成“过一点，有多条直线与已知直线平行”，是不是也可以改成“ 过一点，没有直线与已知直线平行 ”呢？

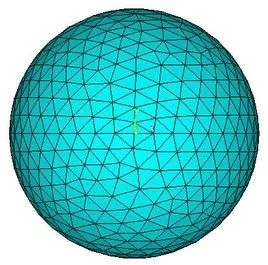
于是，有个叫 黎曼 的聪明人，结合欧式几何的前四条公里加上“ 过一点，没有直线与已知直线平行 ”创建了自己的几何—— 黎曼几何。

比如，在一个球面上，过直线外一点所画的直线一定与已知直线相交。

所以黎曼几何又称 椭球几何 。

##可能会有人说地球仪上的纬线是平行的呀？！但是注意曲率展开后的纬线是弯的，纬线上任意两点最短连线不是纬线本身，当然赤道除外。球面上的直线只有大圆。

在航海学上黎曼几何也得到了广泛应用。地球本身就是曲面的，如果使用欧式几何，只会得到错误的结论。