10道变态难数学题 盘点10大仍未解开的数学难题(5)

10道变态难数学题

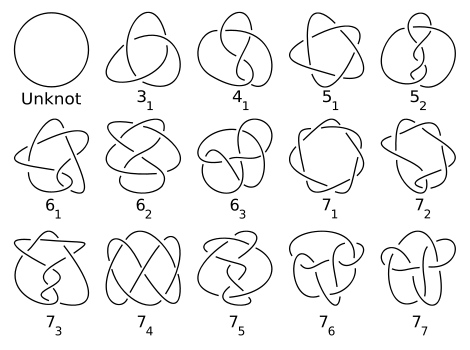
在数学中，活结死结问题是在给定某种结的情况下在算法上识别不打结的数量。

将绳子的两端在无穷远处接起来，就形成了拓扑学意义上的纽结。如果这个纽结与一个圈在某种意义上拓扑等价，数学上称之为unknot，就意味着原来的结是活结，否则就是死结。

在过去的20年中，已经为出现了几种计算机算法，它们能够解开复杂的结，但是随着结变得越来越复杂，算法花费的时间越来越长。

有数学家认为算法可以消除任何打结，而另外的人证明这是不可能的，他们认为“活结死结问题”的计算强度不可避免的加大，导致无法消除打结。

8.大基数

如果您从未听说过大基数，请准备学习。在19世纪末，一位名叫格奥尔格·康托尔的德国数学家确定了在两个集合中的成员，其间一对一关系的重要性，定义了无限且有序的集合，并证明了实数比自然数更多。

康托尔对这个定理所使用的证明方法，事实上暗示了“无限的无穷” 的存在。

在集合论的数学领域中，大基数性质是有限基数的一种性质。顾名思义，具有这种性质的基数通常非常“大”，它们不能在最普遍的集合论公理化中得到证明。

最小无穷大，记为ℵ₀。那是希伯来语字母aleph；它的读数为“ aleph-零”。它是一组自然数的大小，因此被写为|ℕ| =ℵ₀。

接下来，一些常见集合大于大小ℵ₀。康托尔证明的主要示例是实数集更大，用|ℝ|>ℵ₀表示。

对于真正的大基数，数学家不断发现越来越大的基数。这是一个纯数学的证明过程，就像有人说：“我想到了一个基数的定义，我可以证明这个基数比所有已知的基数都大。”

然后，如果他们的证明是正确的，新的最大的已知大基数就此诞生，直到有人提出更大的基数证明。

在整个20世纪，已知的大基数稳步向前发展。从某种意义上说，大型基数层级的顶端已可见。一些定理已经被证明，对大基数的可能性施加了某种限制。但是仍然存在许多悬而未决的问题。

9. + e？

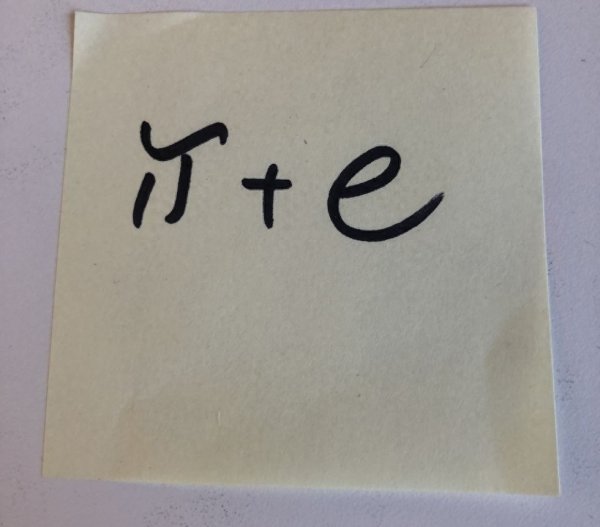
鉴于我们对数学中最著名的两个常数和e所了解的一切，这真让人惊讶，将它们加在一起时令数学家们困惑。

这个问题全是关于代数实数的。定义：如果实数是某些具有整数系数的多项式的根，则实数是代数的。例如，x²-6是具有整数系数的多项式，因为1和-6是整数。

x²-6= 0的根是x =√6和x =-√6，这意味着√6和-√6是代数数。

所有有理数和有理数的根都是代数的。所以可能感觉“大多数”实数都是代数的，结果却恰恰相反。

实数可以追溯到古代的数学，而e是从17世纪才开始出现的。

好吧，我们确实知道和e都是超越数。但是，我们不清楚 + e是代数的还是超越数。

同样，我们不了解e， / e及其它们的其他简单组合的结果性质。因此，关于我们几千年来知道的数字仍然存在着令人难以置信的基本问题，这些问题仍然是神秘的。

10.是有理数吗？