np是什么意思呢 数学中的最著名的难题P=NP(2)

np是什么意思呢

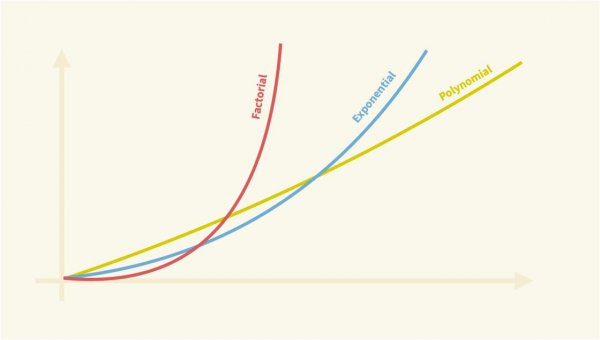
一个算法的时间复杂度被描述为一个渐近函数，它依赖于算法的输入大小。一个主要的区别是阶乘，指数和多项式复杂度函数。

对于具有多项式复杂度的算法和具有更基本复杂度函数的算法，有一个基本的区别。这种区别主要是由于多项式增长被认为比其他增长更为缓慢，因为增大输入不会导致所需步骤急剧增加。

多项式（Polynom）是一种只涉及加、减、乘和非负整数指数运算的构造，因此不是指数或阶乘增长。选择多项式来表示有效的计算似乎是任意的，然而，随着时间的推移，它从许多角度证明了自己的合理性。

例如，多项式在加法、乘法和组合下的闭包保留了自然编程实践中的效率概念，比如将程序链接到一个序列中，或者将一个程序嵌套到另一个程序中

具有多项式时间复杂度的算法被称为“高效”。

多年来，为了有效地解决哈密顿循环决策问题，科学家们进行了许多尝试。其中一种是Held-Karp算法，它能在指数时间内解决这个问题。然而，没有已知的算法可以在多项式时间内解决这个问题，因此，它仍然被认为是一个难题。

迈克尔·赫尔德，理查德·史克和理查德·卡普。

然而，一个有趣的现象发生了，尽管我们不能有效地解决这个问题，给定一个路径图中，我们至少可以有效地检查是否是哈密顿循环，因为简单循环中的最大顶点数为n，则遍历路径所需的时间被多项式限定为n。。

这种现象也出现在其他难题中，例如数独决策问题——给定一个不完整的数独网格，我们希望知道它是否至少有一个有效的解决方案。

任何提出的数独解决方案都可以很容易地验证，并且随着网格的增大，检查一个解决方案的时间会多项式的增长。然而，所有已知的寻找解决方案的算法，对于困难的例子，时间会随着网格的增大呈指数增长。

与哈密顿路径决策问题相似，目前还没有任何已知的算法可以有效地解决数独问题，但是，只要给出一个解，就可以有效地验证该解。

似乎许多其他决策问题都具有这一特性——不管它们是否能被有效地解决，它们所提出的解决方案都能被有效地验证。这类问题被定义为NP。

如果一个决策问题的解能被有效地验证，那么这个决策问题就是NP问题。

首字母缩写NP代表不确定性多项式时间（尽管人们普遍认为NP的意思是“非P”）。

进一步思考问题的可解性与其解的可验证性之间的关系，我们可以得出下一个结论：如果一个决策问题是有效可解得，那么它的解必须是有效可验证的。

为什么？因为如果一个决策问题是可以有效地解决的，那就意味着我们可以有效地找到它的解决方案。

然后，给出一个解决方案，我们可以简单地通过与问题的实际解决方案比较来验证它。换句话说，生成解决方案的算法的正确性自动证明了该解决方案。

从这个结论可以看出，很明显，NP包含的问题子集也是有效可解的。这个子集被定义为P。

P是所有可有效解决的决策问题的集合，是NP的一个子集。基本算法是多项式时间可解的。象棋决策问题不属于NP问题，因为没有一种有效的算法可以检查给定的棋盘是否有效。魔方决策问题属于NP问题，因为判断一个给定的魔方是否是一个解是很简单的。

哈密顿路径决策问题有一个有效的算法可以验证它的解，因此，它属于NP。有人可能会问这个问题是否在P中，一方面，我们不知道有一个有效的算法可以解决这个问题。

另一方面，没有证据表明这样的算法不存在。事实上，这样的算法仍然有可能存在，而且还没有被发现。数独的决策问题也是一样。

事实上，对于许多其他主要问题，包括布尔可满足性问题，旅行推销员问题，子集和问题，派系问题，图着色问题——尽管我们已经证明这些问题是NP，但没有证据表明他们在P 。这就是P=NP问题的意义所在：

P和NP真的是一样的吗？

如果是的话，这就意味着NP中的所有问题都可以被有效地解决，尽管我们仍然没有找到实现这一点的神秘算法。否则，在NP中存在一些无法有效解决的问题，任何尝试解决将意味着浪费我们的时间和精力。

大多数时候，不能有效地解决问题是一件消极的事情。然而，在某些情况下，我们可以从问题的“硬度”中获益。属于NP而不属于P的问题，其主要特点是很难解决，但很容易验证其解决方案。

给定两个正整数n和k，判断n是否有一个质因数小于k。——质因数分解决策问题

由于该问题的解可以有效地验证，因此我们知道该问题属于NP，给定一个整数c，它需要“多项式时间”来知道c是否是一个比k小的质数，还是n的因数。

但是，目前还没有一种算法可以在多项式时间内解决这一问题。因此，使用两个相当大的质数，就可以计算它们的乘法，这用于生成一个公钥和一个私钥。

公钥可以为所有人所知，并用于加密消息。使用公钥加密的消息只能在合理的时间内使用私钥解密，假设没有有效的方法将一个大整数分解为它的质数因子。