正三棱锥外接球半径万能公式 正三棱锥外接球半径公式的简化版本

正三棱锥外接球半径万能公式

为大家说一说正三棱锥外接球半径万能公式的知识，具体介绍如下：

正三棱锥是一种有四个面的多面体，它有一个底面是正三角形，其余三个面都是三角形。正三棱锥的外接球是指与正三棱锥相切于六个顶点和该多面体的外部的球形。

在解决与正三棱锥有关的问题时，确定正三棱锥外接球的半径非常重要。于是，今天我们来探讨一下正三棱锥外接球半径的万能公式。

什么是正三棱锥外接球？

相信对多数人来说，外接球这个概念让他们头疼不已。正如其名，正三棱锥外接球是一个球形，位于正三棱锥的外部，同时能够接触到该多面体的六个顶点。简单来说，这个球是可以与这个正三棱锥“轻松”接触的。

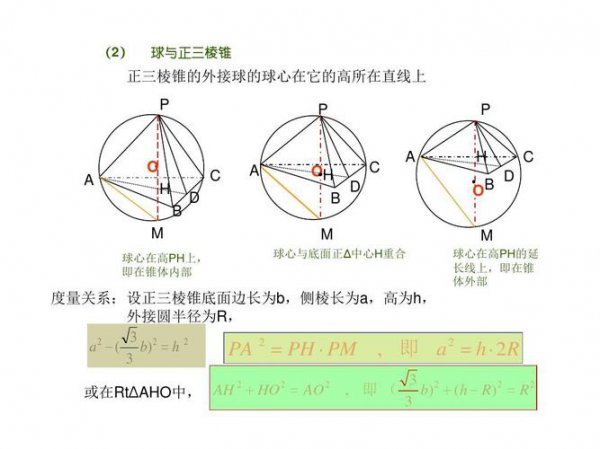
我们可以根据三棱锥的顶点在外接球表面上形成的的四边形面积定理来计算正三棱锥外接球的半径，具体的公式如下：

$r = \frac{1}{6}\sqrt{2}(a^2 + 4h^2)^{\frac{3}{2}}$

其中，a为正三棱锥的棱长，h为正三棱锥高。这个公式的效用不仅仅限于求正三棱锥外接球的半径，还可以用于求任意三棱锥外接球半径。让我们更详细地了解这个公式。

如何推导出万能公式？

为了推导出三棱锥外接球定理，我们需要对勾股定理以及喇叭形的公式有一定的了解。

三棱锥内心位于中心高线上，因此，连接底面正三角形中心点与三棱锥垂心点的线段就是中轴线，且该线段垂直于三棱锥底面中心三角形的平面。

假设一棵正三棱锥的高为h，底边长为a，而垂心到底面的距离为d，那么根据勾股定理，我们可以将中轴线的长度表示为：

$l = \sqrt{h^2 + d^2}$

对于正三棱锥的外接球而言，梯形的一条并边恰好为外接球的直径。根据喇叭形公式，我们可以求得中轴线的长度：

$l = \frac{\sqrt{2(a^2 + 4h^2)}\sqrt{a^2h^2}}{a^2 + 3h^2}$

将这两个公式联系起来，我们可以解出正三棱锥外接球的半径：

$r = \frac{1}{2}\frac{\sqrt{(a^2 + 4h^2)^3}}{a^2 + 3h^2}$

经过简化后，我们可以得到完整的万能公式：

$r = \frac{1}{6}\sqrt{2}(a^2 + 4h^2)^{\frac{3}{2}}$

万能公式的应用

如前所述，万能公式不仅仅用于求解正三棱锥外接球半径，还可用于求解三棱锥外接球半径。只需将公式中的a表示成底边长， h表示为三棱锥的高，这个公式便可以用于求解任意三棱锥的外接球半径。

以下是一个示例：求一个三棱锥，顶角的方位角分别是30度、60度和90度，顶点到棱长的长度为8，那么三棱锥的外接球直径是多少？

首先，我们需要计算出三棱锥的高。由于棱长的长底边是一个正三角形，因此高的长度为线段的一半，即：

$h = \frac{8}{2} = 4$

接下来，我们可以用万能公式求出外接球的半径：

$r = \frac{1}{6}\sqrt{2}(a^2 + 4h^2)^{\frac{3}{2}}$

$r = \frac{1}{6}\sqrt{2}(8^2 + 4\times4^2)^{\frac{3}{2}} \approx 16.396$

因此，该三棱锥的外接球直径为:r x 2 $\approx$ 32.8。

结论

正三棱锥外接球半径万能公式对于解决任意三棱锥外接球半径的问题都非常有用。通过简单的计算，我们可以轻松求出外接球的半径，这对于一些涉及到多面体体积和表面积的问题非常有用。

因此，如果你想深入研究多面体的计算问题，正三棱锥外接球半径万能公式是你不可或缺的一门工具。

上面([领啦网])为您介绍的正三棱锥外接球半径万能公式的全面介绍了，希望给网友们带来一些相关知识。