偏导数存在和连续的关系 偏导数的连续性与存在性相关

偏导数存在和连续的关系

小编为大家讲一讲偏导数存在和连续的关系方面的介绍，一起跟随小编看看具体内容吧！

偏导数是求多元函数在某一点的导数，但是只考虑它在该点与指定方向上的变化率。

当只有一个自变量和一个因变量时，我们可以求出导数为一条切线的斜率。但是当有多个自变量时，导数就成为了一个偏导数。

在多元函数的情况下，我们可以通过对一个变量求导数，而另一些变量保持不变，来得到偏导数。

例如，多元函数$f(x,y) = xy^2$在点$(2,3)$的偏导数就是在$y = 3$时对于$x$的导数，表示为$f_x(2,3)$。同理，在$x=2$时对于$y$的导数表示为$f_y(2,3)$。

偏导数存在的条件

对于一个多元函数$f(x,y)$，如果在某一点$(x_0, y_0)$处，对于$x$和$y$的偏导数都存在，那么我们就可以说在这个点这个函数的偏导数存在。

根据偏导数的定义，我们可以计算出偏导数的表达式，然后判断其是否存在。如果偏导数存在，那么它就具有如下两个条件：

1. 在点$(x_0, y_0)$的邻域内，函数$f(x,y)$必须是连续的。

2. 在点$(x_0, y_0)$的某个邻域内，函数$f(x,y)$必须是可微分的。

这意味着如果$f(x,y)$在一个点处的偏导数不存在，那么在这个点不满足上述条件中的至少一个条件。

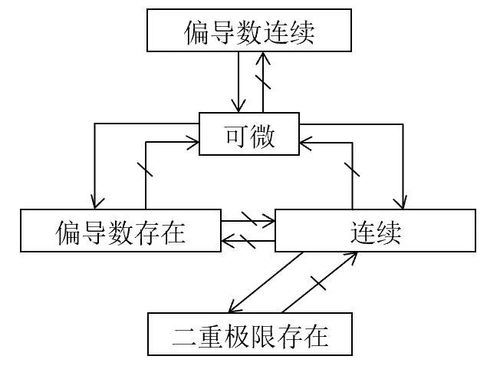
偏导数的连续性

在偏导数存在的情况下，我们还需要判断它们是否连续。如果$f_x$和$f_y$在某个点$(x_0, y_0)$连续，则称它们在该点连续。

我们可以使用偏导数的定义来判断其连续性。对于每个点$(x_0, y_0)$，我们需要找到一个邻域内的任意点$(x, y)$，计算偏导数$f_x$和$f_y$。然后我们需要检查当$(x,y)$趋近于$(x_0,y_0)$时，$f_x$和$f_y$是否趋近于$f_x(x_0,y_0)$和$f_y(x_0,y_0)$。

如果趋近，那么$f_x$和$f_y$就是连续的；否则它们不是连续的。

需要注意的是，偏导数存在并不意味着偏导数连续。一个最简单的例子是，当函数$f(x,y)$的定义为：

$$

f(x,y) = \left\{

\begin{aligned}

\frac{xy^2}{x^2 + y^4}, \quad (x,y) \neq (0,0) \\

0, \quad (x,y) = (0,0) \\

\end{aligned}

\right.

$$

在点$(0,0)$处，我们可以求出$f_x(0,0) = f_y(0,0) = 0$；但是，我们对于任意非零的$(x,y)$，$f_x$和$f_y$都不存在。因此，偏导数存在且是零，但是偏导数并不连续。

总结

偏导数在多元函数求导中有其重要的应用。然而，只有在函数在某个点处可微分且连续的情况下，才能判断偏导数是否存在。如果存在，我们还需要检查其是否连续。

判断偏导数的存在和连续性有许多的方法，但最直接的方法是使用偏导数的定义来进行计算和对比。注意到，当多元函数的偏导数存在时，它的连续性不一定成立，反之亦然。

因此，我们需要在具体的求导中注意判断偏导数的存在和连续条件，并根据需要采取不同的判断方法，以保证求导的正确性。

以上是『领啦网』关于偏导数存在和连续的关系的具体介绍，供网友们借鉴参考。