30 60 90三角形三边关系公式

30 60 90三角形三边关系公式

您可能不了解90三角形三边关系公式及60的内容，具体详情如下：

在几何学中，三角形是一个具有三个顶点和三条边的形状。对于既定的三角形，它们的边长和角度可以明确地规定。其中一种特定类型的三角形是30 60 90三角形，它具有独特的性质和特征。

在30 60 90三角形中，角度大小分别为30度、60度和90度，而这些角度分别对应着边长比例为1:√3:2。

这意味着，若已知一个边长，则可以通过这个比例来计算其他边长。例如，如果已知30 60 90三角形的短边长为1，则长边长为2，斜边长为√3。这种能够根据比例轻松计算出三角形各边的长度的性质，使得30 60 90三角形在数学和工程学中得到广泛的应用。

推导30 60 90三角形的边长比例

要理解30 60 90三角形的边长比例，可以通过以下方法得出：

1. 画出30-60-90度三角形

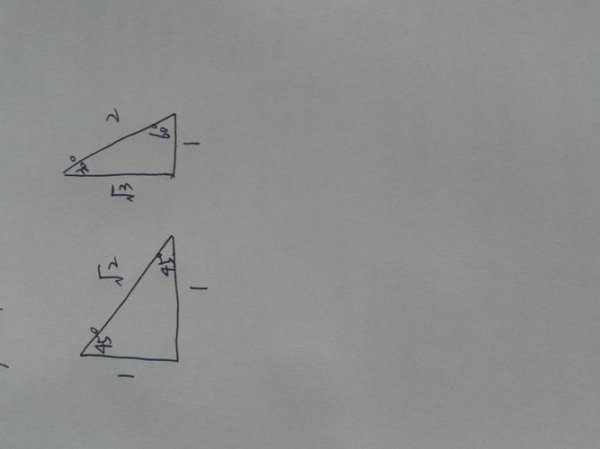
首先，画一个30 60 90度的三角形，如下图所示。在这个三角形中，∠BAC为30度，∠ACB为60度，而∠ABC为90度。


2. 画出三角形的高线

接着，画出从角A垂直于BC的高线AD。由于AD垂直于BC，因此∠BAD为30度，而∠ABD为60度。

3. 使用三角函数计算边长比例

现在，使用三角函数来计算三角形的边长比例。以?ABC为例，可以得出以下关系：

tan 60° = AB / BC

√3 = AB / BC

AB = √3BC

接着，以?ABD为例，可以得到以下关系：

tan 30° = AD / BD

1 / √3 = AD / BD

BD = √3AD

因此，根据?ABC和?ABD两个三角形各自的边长比例，可以得到三角形的边长比例为1:√3:2。

使用30 60 90三角形的边长比例

30 60 90三角形的边长比例可以应用到多种不同的问题中。下面介绍几个常见的例子。

计算不规则三角形的面积

假设我们需要计算一个不规则三角形的面积。如果已知该三角形的一个角度为60度，并且已知角度对应边的长度，此时就可以使用30 60 90三角形的比例来计算该三角形的其他边长。然后，就可以使用海伦公式来计算三角形的面积。海伦公式如下：

s = (a + b + c) / 2

A = √[s(s - a)(s - b)(s - c)]

其中，s是三角形的半周长，a、b和c分别为三角形的三边长。已知边长后，就可以通过海伦公式来计算出三角形的面积了。

设计三角形支架

假设需要设计一个三角形支架，该支架有三条腿，每个角度分别为30、60和90度。已知三角形的高度为h，要求支架的各条腿长度均相等。

此时，可以使用30 60 90三角形的比例来计算出每个腿的长度。根据这个比例，可以得出斜边的长度为2h，水平边的长度为h，而垂直边的长度为h√3。因此，在设计支架的时候，可以根据这个比例来确定各条腿的长度，从而确保支架稳定。

计算斜率

斜率是一个直线的倾斜程度，可以用来表示一个坡度、山峰或其他自然地貌的陡峭程度。30 60 90三角形的比例可以用来计算斜率。

具体来说，如果已知一个山坡的高度和倾斜角度，可以使用30 60 90三角形的比例来计算山坡的斜率。例如，如果已知山坡高度为h、倾斜角度为30度，则可以计算出山坡的水平距离为h√3，从而计算出斜率。

以上就是90三角形三边关系公式、60以及30的全部介绍了希望能给您带来帮助，最后别忘了多来「领啦网」瞧一瞧更多的经验常识！