相似三角形面积比和边长比的关系

相似三角形面积比和边长比的关系

今天带来的生活小经验相似三角形面积比和边长比的关系的生活小知识，下面为您详细介绍

相似三角形是指具有相同形状但大小不同的三角形。在数学中，相似三角形是一个重要的概念，它涉及到面积比和边长比的关系。

相似三角形的定义

首先，让我们明确相似三角形的定义。如果两个三角形的对应角度相等，那么这两个三角形就是相似的。相似的三角形不一定是等边三角形，也不一定是等腰三角形，但它们的形状是相同的。

如果一个三角形与另一个三角形相似，那么这两个三角形的边长比例是相等的。例如，如果两个三角形的边长比例是2:1，那么它们的所有边长都按这个比例缩放。如果边长比例是3:1，那么它们的所有边长都按这个比例缩放。

相似三角形的面积比

在相似三角形中，面积比也是相等的。具体来说，如果两个三角形是相似的，那么它们的面积比等于它们的边长比的平方。

例如，如果三角形ABC和三角形DEF是相似的，它们的边长比为2:1，那么它们的面积比为(2:1)2=4:1。这意味着三角形ABC的面积是三角形DEF的四倍。

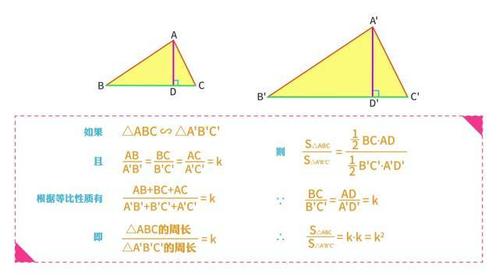
证明相似三角形面积比和边长比的关系

现在我们来证明相似三角形的面积比等于它们的边长比的平方。

首先，设三角形ABC和三角形DEF是相似的，它们的边长比为a:b。因为它们是相似的，所以它们的对应角度相等。也就是说，∠A=∠D，∠B=∠E，∠C=∠F。

我们可以用三角形的高度和底边来计算它们的面积。设AD和DG分别是三角形ABC和DEF的高，AB和DE分别是它们的底边。

根据三角形的面积公式，三角形ABC的面积为：

SABC=?AB×AD

三角形DEF的面积为：

SDEF=?DE×DG

由于三角形ABC和三角形DEF是相似的，所以它们的高度比也是a:b。因此，我们可以将AD表示为a/b×DG，将DG表示为b/a×AD。

将AD和DG代入三角形ABC和三角形DEF的面积公式中，得到：

SABC=?AB×(a/b)×DG

SDEF=?DE×(b/a)×AD

将AB和DE表示为a和b的倍数，得到：

AB=ak，DE=bk

代入到上面的公式中：

SABC=?ak×(a/b)×DG

SDEF=?bk×(b/a)×AD

化简，得到：

SABC=?ak×a/b×(b/a)×AD

SDEF=?bk×b/a×(a/b)×DG

可以发现，(a/b)×(b/a)=1。因此，上述公式可以进一步化简为：

SABC=?a2/b×AD

SDEF=?b2/a×DG

再次利用三角形相似的性质，得到：

AD/b=DG/a

代入上述公式中，得到：

SABC=?a2/b×DG/a

SDEF=?b2/a×AD/b

进一步化简，得到：

SABC/SDEF=(?a2/b×DG/a)/(?b2/a×AD/b)

SABC/SDEF=a2/b2

上式表明，相似三角形的面积比等于它们的边长比的平方。

结论

在数学中，相似三角形是一个重要的概念。它涉及到面积比和边长比的关系。如果两个三角形是相似的，它们的边长比例是相等的。而它们的面积比则等于它们的边长比的平方。

相似三角形的面积比和边长比的关系可以通过数学的方法进行证明。这是一个基础的数学知识，对于学习几何学和三角函数等高中数学课程有很大的帮助。

上面(「领啦网」)为您介绍的相似三角形面积比和边长比的关系的具体介绍，希望给网友们带来一些知识。