线面垂直判定 判定线与面是否垂直的定理

线面垂直判定

今天小编介绍判定线与面是否垂直的定理和线面垂直判定方面的经验，一起跟随小编看看具体内容吧！

线面垂直这个知识点如果单独考不会太难，但是在综合性考题中就会有些难度。本篇将给大家详细分享这部分的知识，一起来看下！

一、直线和平面垂直的定义

如果一条直线和一个平面相交，并且和这个平面内的任意一条直线都垂直，我们就说这条直线和这个平面垂直.其中直线叫做平面的垂线，平面叫做直线的垂面.交点叫做垂足.

【注意】：

1.定义中的任意一条直线为所有直线，但与无数条直线不同；

2.直线和平面垂直只是相交的一种特殊形式；

3.直线和平面垂直的定义简称线面垂直，则线线垂直。

二、直线和平面垂直的判定定理

1、判定定理

文字：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。

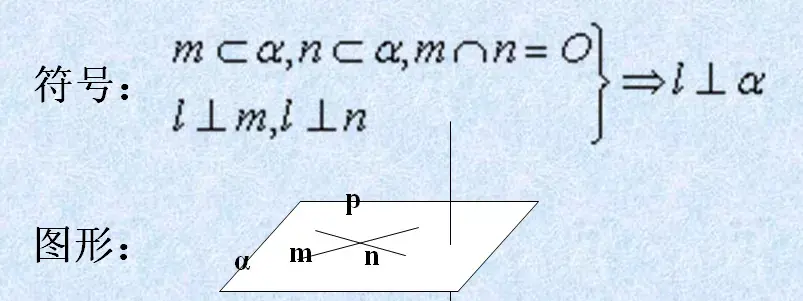
性质是指：如果一条直线垂直于一个平面，那么这条直线垂直于这个平面内的任意一条直线。（此结论经常用）

2、直线和平面垂直的画法

通常把直线画成和表示平面的平行四边形的一边垂直。

3、线面垂直直观图的画法：

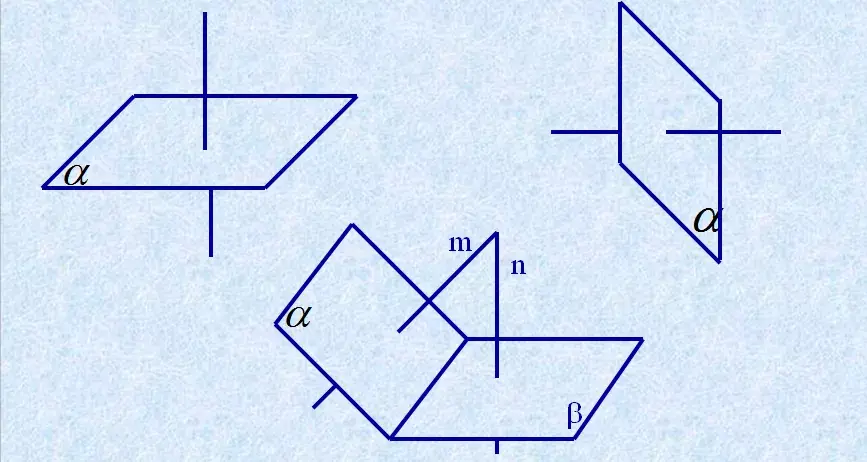
三、推理模式

如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。

推理过程：

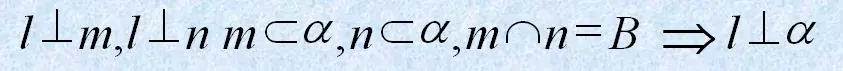
线线垂直 ——> 线面垂直

【例题演练】

如图，正方体ABCD－A1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，求证：B1H⊥平面AD1C.

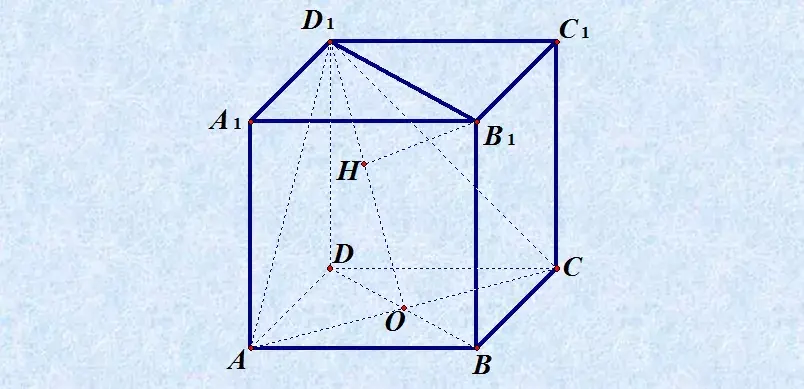
证明：连接B1D1，

∵ B1B⊥AB，B1B⊥BC，

∴ B1B⊥平面ABCD，

∴ B1B⊥AC，

∵ 又AC⊥BD， ∴ AC⊥平面BB1D1D，

又B1H平面BB1D1D，∴ AC⊥B1H，

又B1H⊥D1O，∴ B1H⊥平面AD1C.

小结

要判断一条直线和一个平面是否垂直，取决于在这个平面内能否找出两条相交直线和已知直线垂直，至于这两条相交直线与已知直线是否有公共点，无关紧要。

以上分享的判定线与面是否垂直的定理及其线面垂直判定的相关内容，希望对您有所帮助！