奇函数的特性与特点 剖析奇函数的性质和特点

奇函数的特性与特点

这些你知道吗？剖析奇函数的性质和特点和奇函数的特性与特点的生活小经验，很不错的经验小知识，建议收藏哦！

什么是奇函数

在数学中，一个函数被称为奇函数，当且仅当它满足以下性质：

对于任何实数x，函数值f(-x)=-f(x)，即函数在对称轴x=0处是对称的。

奇函数的导函数为偶函数。

奇函数在区间[-a,a]上的积分值为0。

下面我们来一一剖析这些性质。

奇函数的性质

1. 对称性

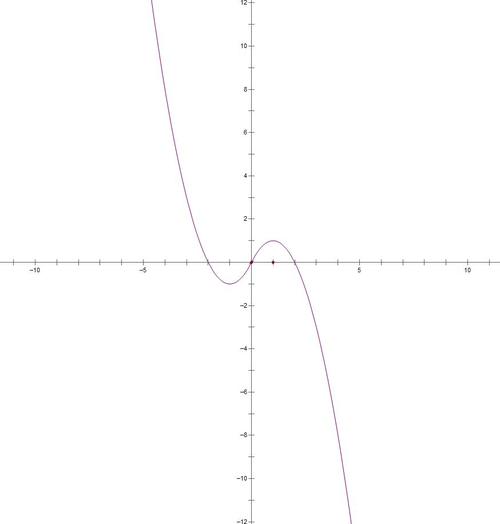
奇函数在对称轴x=0处是对称的，这意味着当x为正数时，函数值与x为负数时的函数值是互相对称的。我们来举一个例子来说明：

如上图所示，奇函数在对称轴x=0处对称，一个点(x,f(x))关于原点对称的点是(-x,-f(x))。

2. 导函数的性质

奇函数的导函数是偶函数，也就是说，对于函数f(x)，它的导数f'(x)满足以下式子：

这个性质非常重要，因为利用这个性质我们可以简化一些复杂的计算。

3. 积分为0

奇函数在区间[-a,a]上的积分值为0，这也是奇函数一个很重要的性质。更一般地，如果f(x)是奇函数，那么在区间[-a,a]上，f(x)的积分可以表示为：

这个公式非常有用，因为我们可以很方便地利用这个公式计算奇函数在某个区间上的积分。

奇函数的特点

1. 对称性

奇函数的一个非常显著的特点就是对称性。这意味着当我们知道了一个点(x,f(x))的函数值，我们就可以很容易地计算出关于x轴对称点(-x,-f(x))的函数值。

2. 线性组合

奇函数在线性组合下保持奇性，也就是说，如果我们有两个奇函数f(x)和g(x)，那么它们的线性组合kf(x)+g(x)仍然是一个奇函数（其中k是任意常数）。

3. 无偏性

奇函数在区间[-a,a]上的积分值为0，这个特点可以看作是奇函数的一个无偏性（mean-free property）。这意味着，当我们在某个区间上对一个奇函数进行积分时，积分值的平均值为0。

4. 奇函数的例子

下面列出一些常见的奇函数的例子：

正弦函数：f(x)=sin(x)

反正切函数：f(x)=tan?1(x)

自然对数函数的导函数f(x)：f(x)=1/x

无穷级数的和函数：f(x)=∑anx? （当该级数中只有奇次幂项时）

结论

奇函数是一类重要的数学函数，具有对称性、线性组合性、无偏性等多种特点。在求导、积分等问题中，我们可以利用奇函数的性质来简化计算过程。此外，在实际问题中，我们也可以利用奇函数来描述一些对称性问题，如交错电流、声波、震荡等。

以上是[领啦网]关于剖析奇函数的性质和特点、奇函数的特性与特点的详细讲解，希望本文能给你带来生活上的帮助！