圆内接四边形的特性 介绍圆内接四边形的性质特点

圆内接四边形的特性

今天分享：介绍圆内接四边形的性质特点和圆内接四边形的特性的相关介绍，很不错的经验小知识，建议收藏哦！

什么是圆内接四边形

圆内接四边形指的是四边形的四个顶点都在同一个圆的周上。这样的四边形常见于几何学中，并且它们有着许多特殊的性质和特点。今天，我们就来介绍一下圆内接四边形的性质和特点。

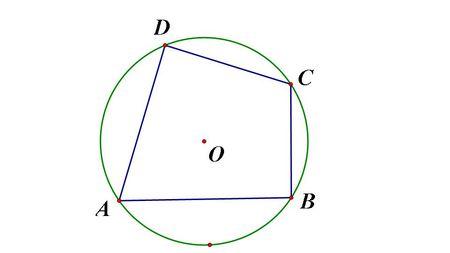
性质一：对角线互相垂直

圆内接四边形的对角线一定互相垂直。具体地说，如果ABCD是一个圆内接四边形，那么对角线AC和BD互相垂直。

证明：

由于圆内接四边形的四个顶点都在同一个圆的周上，因此它们满足欧拉定理：相对顶点的角的余弦乘积相等。即：

$cos∠A×cos∠C=cos∠B×cos∠D$

同时，由于对角线AC和BD相交，我们可以得到：

$cos∠A×cos∠C+cos∠B×cos∠D=0$

这个式子表明，如果对角线互相垂直，那么它们的余弦值的乘积为负数。因此，对角线AC和BD互相垂直。

性质二：对角线互相平分

圆内接四边形的对角线一定互相平分。具体地说，如果ABCD是一个圆内接四边形，那么对角线AC和BD互相平分。

证明：

首先，我们可以证明ABCD是等腰梯形。由于它是圆内接四边形，因此：

$∠CBA=∠CDA$

由于相邻角相等：

$∠CAB=∠ACB$

对角线AC和BD相交，我们可以得到：

$∠(AC,BD)=∠A+(∠B-∠A)/2+(∠C-∠D)/2=90°$

同时，我们可以得到：

$∠BAC=∠BDC$

因此，三角形ABC与三角形CDA相似，三角形ABD与三角形BCD相似，从而可以得到对角线AC和BD互相平分。

性质三：对角线长度相等

圆内接四边形的对角线长度相等。具体地说，如果ABCD是一个圆内接四边形，那么对角线AC和BD的长度相等。

证明：

由于四个顶点都在同一个圆的周上，因此：

$∠AOC=2∠ABC，∠COD=2∠CDA$

由于对角线AC和BD平分，我们可以得到：

$∠ABC=∠CDA，∠BAD=∠BCD$

因此，我们可以得到：

$∠AOC=∠COD，∴ AC=BD$

性质四：内角和为360度

圆内接四边形的内角和为360度。具体地说，如果ABCD是一个圆内接四边形，那么它的四个内角的和为360度。

证明：

由于四个顶点都在同一个圆的周上，因此：

$∠AOC=2∠ABC，∠COD=2∠CDA$

从而可以得到：

$∠AOC+∠COD=2∠ABC+2∠CDA=360°$

同时，由于ABCD是等腰梯形，我们可以得到：

$∠B=∠C， ∠A=∠D$

因此，我们可以得到：

$∠AOC+∠BOD=∠A+∠D=360°$

因此，圆内接四边形ABCD的四个内角的和为360度。

性质五：对角线的中点连成的线段是圆的直径

圆内接四边形的对角线的中点连成的线段是圆的直径。具体地说，如果ABCD是一个圆内接四边形，那么对角线AC和BD的中点连成的线段是圆的直径。

证明：

由性质二可得，AC和BD的中点分别为O1和O2，则OO1与OO2分别对应于∠ABC和∠ACD，因此它们互补，它们的和为180度。因此，OO1、AC、O2O1和BD构成的四边形是一个反中心四边形，从而OO1和O2O1是圆的直径。

结论

圆内接四边形具有以上五个基本性质，这些性质不仅可以被用来解决与圆内接四边形相关的问题，还常常用于证明别的几何定理。因此，圆内接四边形是几何学中的重要概念，它的性质和特点值得我们深入学习和探究。

上述就是介绍圆内接四边形的性质特点和圆内接四边形的特性的具体内容，如果能给您带来帮助，记得常来「领啦网」网！