三角形重心的性质有哪些 三角形重心的三个重要性质讲解(2)

三角形重心的性质有哪些

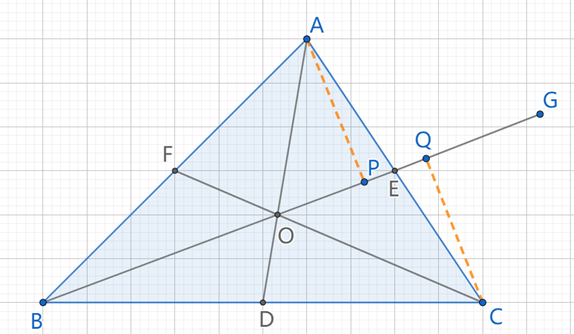
过A做AP⊥BE于P，过C做CQ⊥BE延长线于Q。

因E是AC中点，AE=CE，由AAS定理易得△AEP≌△CEQ

因此AP=CQ

S△AOB：S△BOC=AP：CQ=1，因此S△AOB=S△BOC

3.三角形的重心是三角形内到三边距离之积最大的点。

如图，O是△ABC内一点，O到三条边的距离分别为h₁、h₂、h₃。

求证：当O为△ABC的重心时，h₁•h₂•h₃取最大值

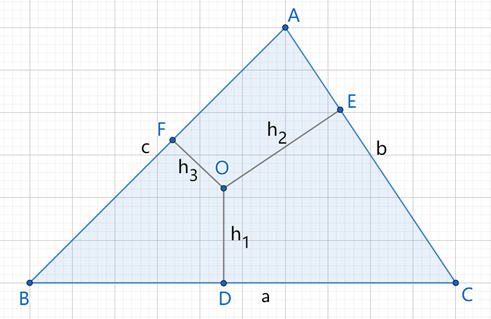
证明：设三角形三条边长分别为a、b、c，连接AO、BO、CO。

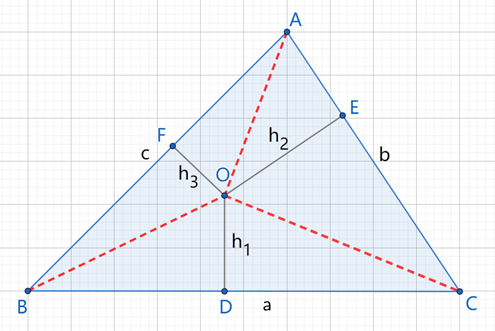
S△ABC= S△AOB+ S△BOC+ S△COA =1/2（a•h₁+b•h₂+c•h₃）

给定了△ABC，那么S△ABC是定值，三边长a、b、c也是定值。

变化的是O的位置，也就是h₁、h₂、h₃是变量。

若求h₁•h₂•h₃的最大值，那么最直观的是使用基本不等式。

利用不等式的思想就是：“将变量向定量上凑”。

因为给定的定量是三角形的边长和面积，那么就要凑出

h₁•h₂•h₃≤X（X是定值）的形式，且一定是朝着

S△ABC=1/2（a•h1+b•h2+c•h3）的方向做变换

积与和之间的基本不等式为：几何平均数≤算数平均数

当有两个变量时，其形式为：