快速系鞋带方法 简述关于系鞋带哪种方法最省事的问题(2)

快速系鞋带方法

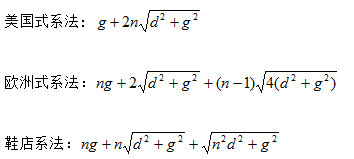
在 n, d, g 的值不同的情况下，这 3 个函数哪一个最大呢？选几个数带进去算算就知道了。假设鞋有 8 对鞋孔( n = 8 )，鞋孔间距离是 1 厘米( d = 1 )，左右鞋孔间的距离是 2 厘米( g = 2 )，这 3 种系法所需要的鞋带长度分别是：

美国式系法：38厘米。

欧洲式系法：40厘米。

鞋店系法：42厘米。

如果按照一条 60 厘米的鞋带的价格 1 元算的话，采用美国式系法可以比第 3 种系法为你节省一大笔钱：（R-M-B） 0.07 元。

再试试其他型号的鞋子，几乎每次都是美国式系法都可以击败另外两种系法，美国式系法似乎应该是 3 种之中是最好的，那是不是在所有的系法中它都是最好的呢？

最优鞋带系法和光线传播的联系

其实，这个问题和光线反射与折射问题有着很巧妙的联系。光在传播的时候有个“怪癖”，总是“抄近道”，选择走最短的路径（当然，死理性派知道这种说法是不严谨的 ）。

我们就知道光的入射角等于反射角，但是可能很少人想过这个现象背后更深层的原因：因为只有这样，才可以保证光线总能以最短的路径达到目的地。

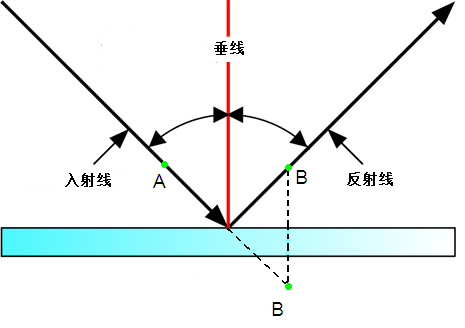
比如下面的图中，A点在入射光线上，B点在反射光线上，AB两点之间相当于有一条直线连接，“两点之间，线段最短”，如果入射角不等反射角，经过AB两点的光线就未必可以保证走的路最短。

回到鞋带的问题上，鞋带在两排鞋孔之间来回穿梭相当于光线在两面相对的镜子之间反射来反射去。

而美国式系法恰好相当于光线以入射角等于反射角的方式进行来回反射（第 n 个鞋孔除外），自然保证了是三种方式中最省鞋带，也是所有可能方式中距离最短的系鞋带方法。

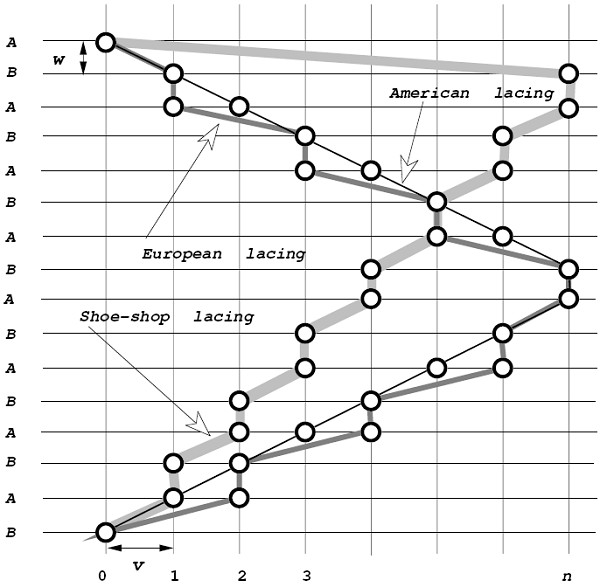
在下面的这幅图里，每一条横线交替代表左边的一行鞋孔（ A ）和右边 ( B )一行鞋孔，竖线代表第 1,2,3,……n 个鞋孔。我们可以在一个平面上清楚地看到这三种鞋带系法是怎样穿过所有的鞋孔的。美国式系法几乎是直线，而另外两种系法曲曲折折，走的距离长也就不出乎意料了。

更省鞋带的非主流系法

看到这里你可能会问，是谁这么闲研究了这样让人想不到的问题？其实以上的系鞋带指南出自一篇论文，下图是这篇奇特的论文的作者，美国北卡罗莱纳大学的 John H. Halton 大叔。